Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 32

             V(x) = - e²Z_l exp[-λ(x- a/2)/4π(x–a/2)ε₀ при a/2 ≤ x ≤ a.                    (5.107)

Для определения первой добавкой V₀ к энергии свободных электронов получаем

V₀ = - e²Z_l exp[-λa/2)/πε₀a.                                                (5.108)

Для решения уравнения (5.98), учитывающего взаимодействие электронов между собой

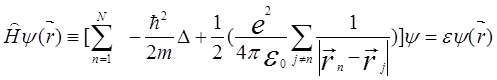,         (5.109

следует использовать многоэлектронную функцию , зависящую от координат каждого электрона и его спина . Существует приближенный метод решения уравнения (5.109), носящий названия метода Хартри-Фока [?], который позволяет получить добавки к энергии свободных электронов за счет взаимодействия их с ионами решетки и между собой. В рамках этого подхода внутренняя энергия может быть записана в виде

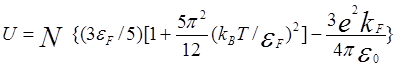.                              (5.110)

где .

С учетом взаимодействия электронов с ионами решетки и между собой для внутренней энергии имеем

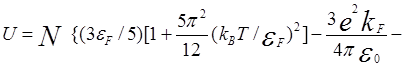- e²Z_l exp[-λa/2)/πε₀a}.     (5.111)

Уравнения состояния электронной подсистемы (5.39) теперь запишем в виде

P = (2/3) 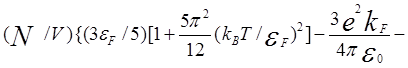e²Z_l exp[-λa/2)/πε₀a}, (5.112)

Аналогичным образом (см. раздел 5.2) может быть найден вклад взаимодействия электронов с ионами решетки и между собой для других термодинамических функций.

5.5. Зонная теория электронов в кристалле и классификация твердых тел

Обратимся теперь снова к картине энергетических зон в кристаллических твердых телах. Оказывается, такая картина дает возможность объяснить качественно многие свойства твердого тела, даже не зная деталей структуры энергетических зон. В частности, зонная схема позволяет классифицировать твердые тела по типу заполнения их энергетических зон электронами на металлы, полуметаллы, диэлектрики и полупроводники.

Определенное заполнение энергетических зон электронами связано с тем, что каждая зона имеет лишь конечное число состояний, а именно 2N, где N — число элементарных ячеек в теле. Если электронов достаточно много, то они каким-то образом будут заполнять эти состояния (напомним, что при Т = 0электроны заполняют все нижние состояния от нуля до энергии Ферми ). В принципе после того, как электроны распределились по энергетическим состояниям, имеются две возможности: либо уровень Ферми совпал с верхней границей одной из разрешенных зон, так что некоторые зоны полностью заполнены, другие полностью свободны, либо уровень Ферми попадает внутрь разрешенной зоны, которая в этом случае заполняется лишь частично. Если бы не существовало отмеченного выше эффекта перекрытия зон разрешенных состояний, то в случае нечетного числа электронов в элементарной ячейке всегда существовала бы частично заполненная зона, поскольку в зоне может разместиться лишь четное (2N) число электронов. В случае четного числа электронов в элементарной ячейке может быть лишь ситуация полного заполнения (показать). Однако на самом деле при учете эффекта перекрытия зон гораздо чаще наблюдается ситуация частичного заполнения. Ниже будет рассмотрена на этой основе классификация твердых кристаллических тел.

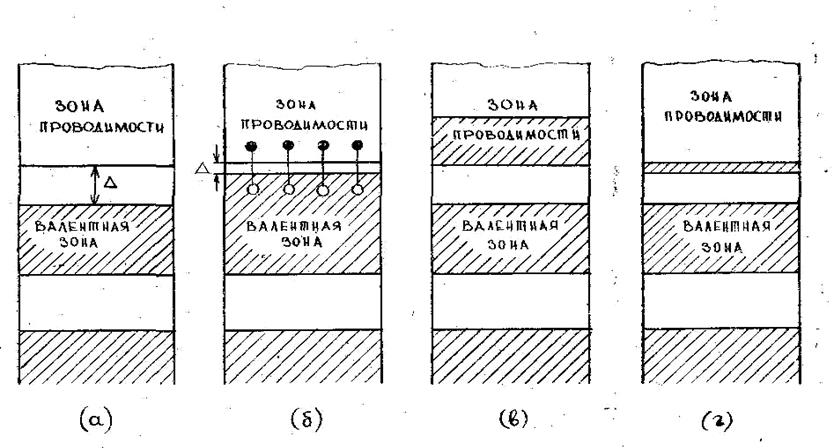                                                 Рис. 5.13

а) Диэлектрики

Если последняя из разрешенных зон полностью заполнена электронами, но все более высокие по энергии зоны целиком свободны, то такие твердые тела являются диэлектриками (изоляторами). Типичными диэлектриками являются Ar, He, Ne, B, C (алмаз), Kr и др. На рис. 5.13а показана энергетическая щель  большой величины (рис. 5.13а). Для типичного диэлектрика — алмаза —   5,4 эВ6,3. При приложении электрического поля к такому телу (при T= 0) электроны из целиком заполненной зоны не могут перейти в разрешенную, так как энергия, сообщаемая им полем, не достаточна для преодоления запрещенной зоны. Отметим, что обычно последнюю заполненную зону называют валентной, а последующую частично заполненную — зоной проводимости. Если T, то имеется малая вероятность части электронам перейти в зону проводимости вследствие термического возбуждения (пропорционального ). Однако для разумных температур (ниже, например, температуры  плавления) концентрация электронов в зоне проводимости пренебрежимо мала и не может вызвать заметную проводимость. На рис. 5.13 показана зависимость энергии от волнового числа для двух зон в диэлектрике (здесь и далее зависимости для валентной зоны и зоны проводимости изображены для двух (вообще говоря, различных) направлений в -пространстве; состояния, заполненные электронами, заштрихованы).