Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 5

a=n_j .                                                  (1.1)

где n, — целые числа. Обычно в качестве основных вектороввыбирают наименьшие по длине в данном направлении. Такие основные векторы называют трансляционными периодами кристаллической решетки. Параллелепипед, построенный па основных трансляционных периодах решетки , j= 1.2.3, носит название элементарной ячейки. Множество элементарных ячеек можно характеризовать размерами граней a₁, a_2, a₃и углами между ними α,β,γ ( рис. 1.5.а). Набор всех векторов трансляции для данного кристалла   образует пространственную решетку – решетку Бравэ (A. Bravais). Если в кристалле выделить какую либо точку A(), находящуюся на расстоянии  от начала координат O, и перейти в точку B (+ ), находящуюся на расстоянии +  от начала координат O, (рис. 1.5.б), то эти точки будут обладать одинаковыми свойствами (например, они могут быть центрами симметрии молекулы, или в них могу находиться частицы одного сорта). Совокупность всех эквивалентных точке A точек кристалла (т.е. отстоящих от нее на вектор трансляции) образует кристаллическую решетку. Сама решетка вместе с расположенными одинаковым образом возле каждого эквивалентного узла атомами (молекулами, ионами) образуют кристаллическую структуру. На рис. 1.5.б показано расположение атомов 1, 2 , образующих кристалл, относительно эквивалентных узлов решетки A и B,  _,  - векторы, определяющие расположение атомов 1 и 2, относительно эквивалентных узлов решетки A и B.

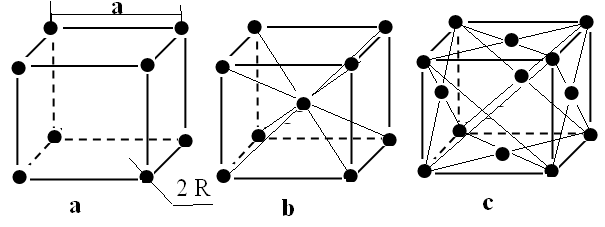
Рис. 1.6

Приведем примеры трех простейших решеток Бравэ (рис. 1.6): a — простая кубическая решетка; b — объемно-центрированная кубическая решетка (ОЦК); c — гранецентрированная кубическая решетка (ГЦК). Всего существует четырнадцать типов решеток Бравэ (см. [1, 6, 7, 11]).

Представляет интерес рассмотреть плотность упаковки атомов в различных типах кристаллических решеток. Под плотностью упаковки понимают относительный объем элементарной ячейки размером а, заполняемой атомами, которые представляют в виде твердых шариков радиусом R. В зависимости от характера расположения атомов (типа кристаллической решетки) плотность упаковки может изменяться.

В простой кубической решетке (ПК) в элементарной ячейке имеется всего один атом, поэтому размер ячейки совпадает с диаметром частицы, образующей кристалл . Плотность упаковки равна:

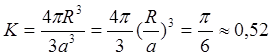
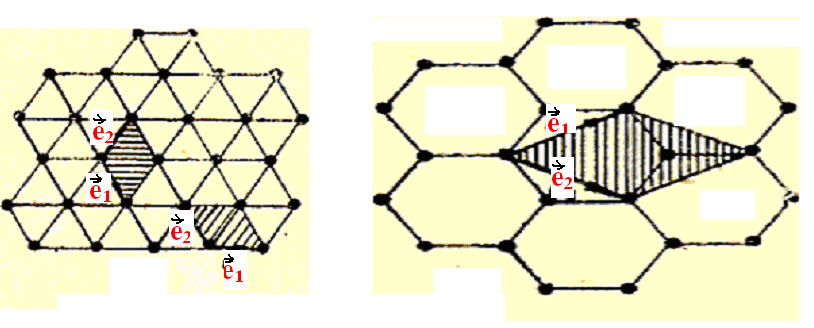              Рис. 1.7.а                                           Рис.1.7.б

Отметим, что простую кубическую решетку при нормальных условиях имеет только α-фаза полония.

Нетрудно показать, что выбор основных векторов, а значит и элементарной ячейки, неоднозначен. На рис.1.7.а показаны различные возможности такого выбора на примере плоской решетки. Если вершина элементарной ячейки совпадает с одним из атомов (узлом решетки), тогда а_:, соединяют ближайшие эквивалентные узлы решётки в соответствующих направлениях. Объем элементарной ячейки определяется как смешанное произведение вида

V_e=•.                                                    (1.1)

и является неизменным, несмотря на неоднозначность выбора элементарной ячейки (показать),

Элементарные ячейки могут быть двух типов — простые и сложные. В простой ячейке имеется атом только одного типа (по своему химическому типу пли геометрическому положению), а в сложной — произвольное число атомов. Отличие простой решетки от сложной видно на рис. 1.7б, где показана плоская решетка. Решетка 1.7.а является простой (в ячейке, образованной основными векторами  и  лишь один атом), а решетка 1.7.б — сложной.По своим физическим свойствам указанные два типа решеток могут существенно отличаться. Например, такое отличие проявляется и в особенностях колебаний решеток.

Несмотря на неоднозначность выбора элементарной ячейки кристалла, существует, метод, который не только позволяет ликвидировать неоднозначность построения элементарной ячейки, но и позволяет учесть все

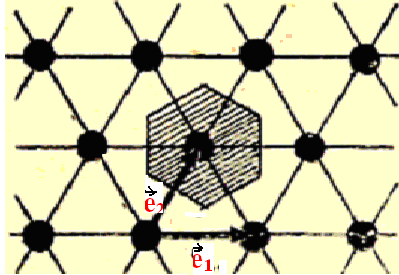
Рис. 1.8