Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 4

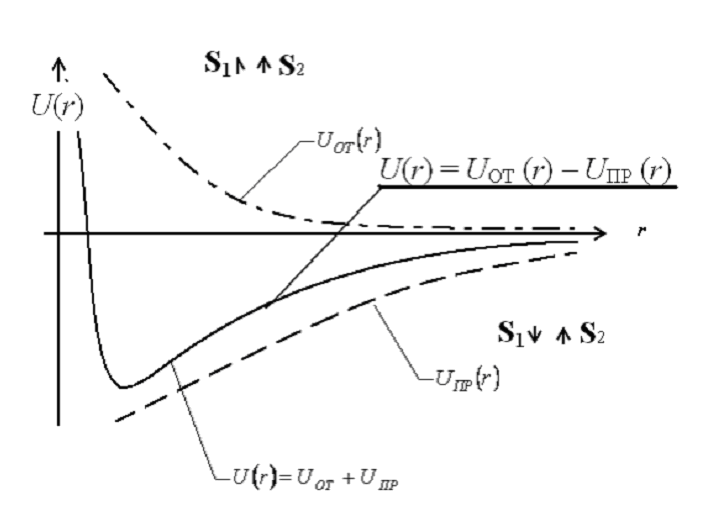
Рис. 1.1

данным типом взаимодействия Na-Cl, в котором Na при взаимодействии отдаёт свой электрон и становится соответственно положительным ионом, а Cl принимает этот электрон и становится отрицательным ионом.

U(r) = U_ОТ(r) – U_ПР(r) = ε exp(-r/ρ) (eZ)² /4πε₀r.

Характерная энергия связи частиц в кристалле U_св =

3.  Металлическая связь.

Характерна для металлов и связана с тем, что в атоме, который естественно является электронейтральным, есть электроны, находящиеся вблизи ядра и есть электроны, находящиеся на удалённых электронных оболочках. При сближении атомов электроны, находившиеся на внешней электронной оболочке могут переходить от одного атома к другому и становиться коллективными, а атомы превращаются в неподвижные ионы, расположенные в узлах решетки. Характерная энергия связи частиц в кристалле U_св =

4.  Водородная связь.

Для действия этой связи необходимо, чтобы в состав кристалла входил водород. Типичным представителем этого типа взаимодействия является вода (точнее лёд, т.к. речь идёт о твёрдых кристаллах). Характерная энергия связи частиц в кристалле U_св =

Встаёт вопрос, как из такого ограниченного количества типов связей объяснить то разнообразие форм веществ? И как, вообще зная тип и соответственно потенциал взаимодействия найти уравнение состояния вещества и его теплофизические свойства?

Очевидно, что знанием только типа взаимодействия здесь не обойтись. Необходимо прибегнуть к помощи квантовой механики. А именно, для того чтобы найти, какую энергию может иметь система, надо решать уравнение Шрёдингера

.

Где  – оператор Гамильтона, 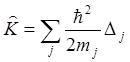– оператор кинетической энергии, – оператор потенциальной энергии, – оператор Лапласа, в котором дифференцирование производится по координатам j-ой частицы. 

 – собственная функция, при воздействии на которую оператором возникает она же, но умноженная на собственное значение энергии  , которое и необходимо отыскать. После определения  можно найти статистическую сумму

 ,

- число состояний с данной энергией. Таким образом, если знаем симметрию кристалла, то знаем число состояний. Зная статистическую сумму и свободную энергию (энергию Гельмгольца) кристалла

 .

можно рассчитать все остальные термодинамические функции. Число состояний с данной энергией, следовательно, это понятие тесно связано с симметрией, которой обладает структура.

1.1.2. Симметрия

Под симметрией понимают инвариантность структур, образующих кристалл, относительно их геометрических преобразований. Среди простейших симметрий частиц, образующих кристалл, отметим следующие.

1)  Трансляционная симметрия, связанная с тем, что сдвиг в некотором направлении на некоторый отрезок длины L_T не изменяет структуру кристалла (рис.1.2)

2)  Симметрия относительно отображения частицы кристалла относительно некоторой  плоскости (рис. 1.3а,б). Рассматривается плоскость P и две частицы Aи B , находящиеся на одинаковом расстоянии от этой плоскости. Причем в случае (1.3.а) это одинаковые частицы, а в случае (1.3.б) – разные

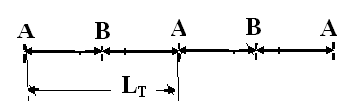
Рис. 1.2

.

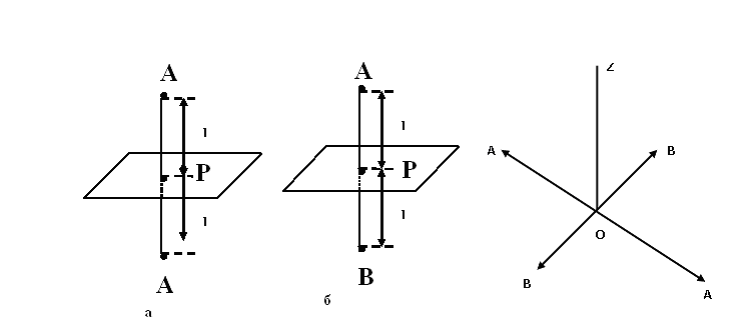
Рис. 1.3                                                Рис. 1.4

Из рисунка 1.3 видно, что в случае (а) отображение относительно плоскости P на ничего не меняет, а в случае (б) отображение приводит к новой конфигурации.

3) Симметрия относительно поворота относительно выделенной оси OZ.

Рассматривается ось OZи четыре частицы A и B (рис.1.4). Видно, что поворот относительно оси на  также сохраняет исходную конфигурацию расположения частиц.

I.2. КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА ТВЕРДОГО ТЕЛА

1.2.1. Геометрическая структура кристаллов. Решетка Бравэ

Кристаллическая структура характеризуется пространственной периодичностью (или, иначе, трансляционной симметрией). Последнее

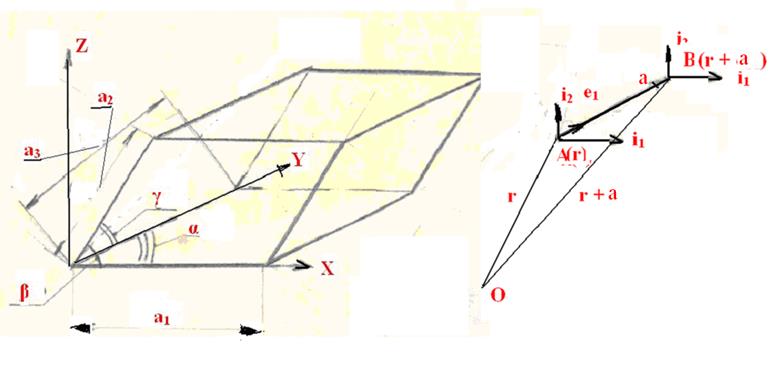                        Рис. 1.5.а                                              Рис. 1.5.б означает, что для любого неограниченного кристалла существует такая тройка неколлинеарных векторов , j= 1.2.3, что смещение кристалла как целого на любой из этих векторов совмещает его с самим собой. Понятно, что таким же свойством обладает и вектор трансляции a