т. е., как уже говорилось, появляется
энергетическая щель ![]() .
Зависимость энергии
.
Зависимость энергии ![]() от
волнового числа
от
волнового числа ![]() (
(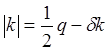 ), отсчитываемого от границ
зоны Бриллюэна, нетрудно получить из (5.70) и записать в виде
), отсчитываемого от границ
зоны Бриллюэна, нетрудно получить из (5.70) и записать в виде
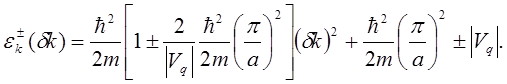 (5.78)
(5.78)
В этом представлении
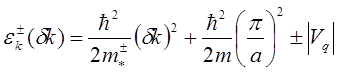 (5.79)
(5.79)
удобно ввести обозначение фиктивные массы электрона, учитывающие взаимодействие с решеткой,
![]() =
= 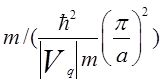 < m,
< m, ![]() =-
=-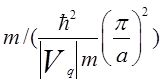 .
.
Из самого приближения слабой связи, в
котором получены приведенные выше результаты, следует, что ![]() ; следовательно
; следовательно ![]() . В таком представлении зависимость энергии
. В таком представлении зависимость энергии ![]() от волнового числа
от волнового числа ![]() (5.78) примет удобный для
интерпретации взаимодействия вид
(5.78) примет удобный для
интерпретации взаимодействия вид
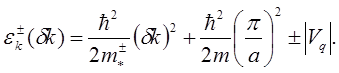 (5.80)
(5.80)
Из представления (5.80) следует, что,
энергия оказывается, как и в случае свободных электронов, квадратичной функцией
![]() , но теперь роль массы
играет эффективная величина
, но теперь роль массы
играет эффективная величина ![]() ,
которую принято называть эффективной массой. Электроны внутри
разрешенной зоны можно трактовать как свободные частицы, но с малой эффективной
массой. Такая трактовка оказывается в ряде случаев очень полезной.
,
которую принято называть эффективной массой. Электроны внутри
разрешенной зоны можно трактовать как свободные частицы, но с малой эффективной
массой. Такая трактовка оказывается в ряде случаев очень полезной.
Итогом рассмотрения приближения слабой связи являются:
а) эффект возникновения зонной картины энергетического спектра;
б) существование узких запрещенных щелей между разрешенными зонами;
в) поведения энергии в зависимости от
импульса вблизи экстремумов энергии происходит по закону ![]() , где эффективная масса меньше
массы электрона, вследствие малой ширины запрещенной зоны
, где эффективная масса меньше
массы электрона, вследствие малой ширины запрещенной зоны![]() ;
;
г) обнаружение сильной интерференции состояний на границе зон Бриллюэна.
5.3.4. Электроны в кристалле (приближение сильной связи)
Второй предельный случай (сильная связь) имеет место, когда электрон сильно связан со своим атомом, находящимся в узле решетки, и лишь за счет туннелирования способен переходить от одного атома к другому. Такая ситуация типична, например, для переходных металлов [6]. Идея метода сильной связи состоит в представлении электронных волновых функции в виде локализованных состояний, которые могут быть найдены из решения уровнения Шрёдингера для изолированного атома. Зная решения для дискретных (локализованных) состояний, можно рассмотреть как изменяются энергетические уровни изолированных атомов при постепенном сближении и объединении в решетку. Из этих же соображений легко понять физический механизм образования зон для сильносвязанных электронов.
Обратимся к формальной стороне метода
[6, 8, 12]. Если атомы сблизились на определенное расстояние, то имеется
конечная вероятность перейти из локализованного состояния одного атома в
локализованное состояние другого, если последнее свободно за счет
туннелирования [10]. При этом, если ![]() — разброс значении энергии
электрона за счет туннелирования,
— разброс значении энергии
электрона за счет туннелирования, ![]() — время пребывания в потенциальной яме «своего»
атома, то из соотношения неопределенности следует
— время пребывания в потенциальной яме «своего»
атома, то из соотношения неопределенности следует
![]() . (5.81)
. (5.81)
Для оценки ![]() воспользуемся формулой [10]
воспользуемся формулой [10]![]() , в которой
, в которой ![]() — период электрона на дискретном уровне;
— период электрона на дискретном уровне;
![]() < 1 — вероятность
перехода в соседнюю потенциальную яму. Отсюда имеем
< 1 — вероятность
перехода в соседнюю потенциальную яму. Отсюда имеем ![]() . Величина
. Величина ![]() , где
, где ![]() — характерная энергия энергетического уровня в
яме и
— характерная энергия энергетического уровня в
яме и ![]() 1. Таким образом, в
такой модели происходит лишь слабое возмущение локализованных (дискретных)
энергетических уровней электронов и это условие противоположно приближению
слабой связи, рассмотренной ранее.
1. Таким образом, в
такой модели происходит лишь слабое возмущение локализованных (дискретных)
энергетических уровней электронов и это условие противоположно приближению
слабой связи, рассмотренной ранее.
При выполнении условия сильной связи
(![]() ) волновая функция может
быть выбрана в виде набора волновых функций дискретного спектра
) волновая функция может
быть выбрана в виде набора волновых функций дискретного спектра
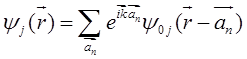 , (5.82a)
, (5.82a)
где ![]() — вектор трансляции, характеризующий
положение n-го атома в узле решетки;
— вектор трансляции, характеризующий
положение n-го атома в узле решетки; ![]() — волновая функция электрона в
изолированном атоме, находящегося в точке
— волновая функция электрона в
изолированном атоме, находящегося в точке ![]() и соответствующая j-ому энергетическому уровню электрона.
и соответствующая j-ому энергетическому уровню электрона.
Сопряженная волновая функция имеет вид
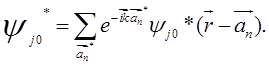 (5.82b)
(5.82b)
Заметим, что выбор волновой функции в виде (5.82) согласуется с теоремой Блоха. Формулу (5.82) можно преобразовать к виду
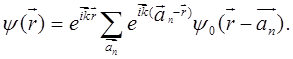 (5.83)
(5.83)
Следовательно, каждая собственная функция, соответствующая j-ому состоянию имеет вид
![]() (5.84)
(5.84)
где 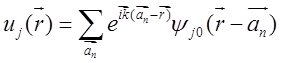 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.