Физика \ Физика твердого тела

Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 27

Среди всех членов суммы отличено от нуля лишь слагаемое, в котором и .

Следовательно, находим

,

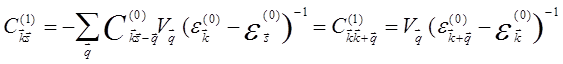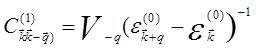.                              (5.61)

Во втором порядке теории возмущений из (5.57c) при  получаем

.

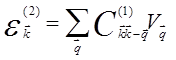Подставляя в  значение из (5.61), находим

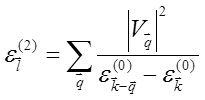 .                                        (5.62)

Таким образом, энергия возмущенного состояния с точностью до членов второго порядка включительно равна

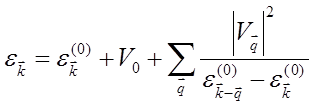                            (5.63)

5.3.3.  Энергетический спектр электронов с учетом взаимодействия с ионами (вырожденный случай слабой связи)

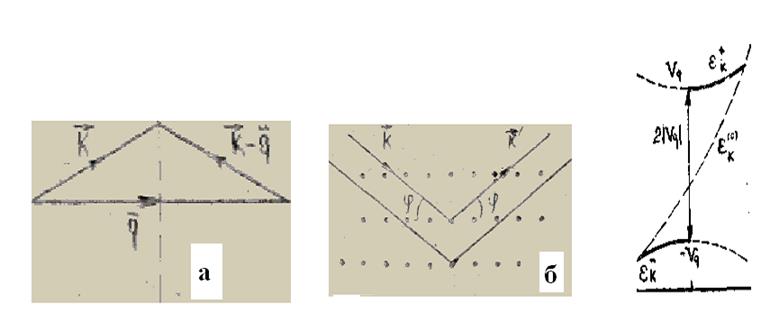
Рис. 5.3                                                   Рис. 5.4

Условием применимости теории возмущений является неравенство 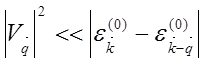 [10].  Вместе с тем это требование не выполняется,  если знаменатель в (5.63) становится малым. Последнее имеет место, когда 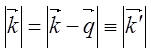. Это условие в одномерном случае может выполняться, когда   приближается к значению (при любом n), поскольку . Таким образом, при  и , т. е. на границе зоны Бриллюэна, теория возмущений в том виде, как она здесь была использована, неприменима из-за того, что энергетический уровень невзаимодействиющих с решетокой электронов двукратно вырожден. В этом случае необходимо применить теорию возмущений с учетом вырождения. В трехмерном случае условие 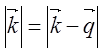означает геометрически, что конец вектора  лежит на перпендикуляре к вектору , проходящем через его середину (рис. 5.3, а). Последнее означает, что вектор  принадлежит границе зоны Бриллюэна. В этом случае и «отказывает» теория возмущений, развитая ранее.

Условие 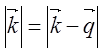имеет и еще одно важное и интересное толкование. Допустим, что электроны рассеиваются на атомах решетки, причем ,— волновые векторы падающих и рассеянных электронов, соответственно. На рис. 5.3, б видно, что условие это можно записать в виде

                                                             (5.64)

где п — целое число;— длина волны электрона; —угол между  и . Соотношение (5.64) представляет ничто иное, как закон отражения Вульфа — Брэгга. Итак, можно сказать, что электроны, длина волны которых удовлетворяет условию Вульфа — Брэгга, испытывают дифракцию на атомах решетки, в результате чего и возникает основное изменение по сравнению со случаем вакуума.

Воспользуемся теперь для рассмотрения поведения энергии электронов вблизи границы зоны Бриллюэна теорией возмущений с вырождением [10]. Пусть, например, имеется лишь двукратное вырождение (для одномерной решетки только такое вырождение и может иметь место). В этом случае, как известно, волновую функцию вырожденного состояния можно представить в виде [10]

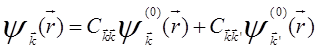.                                   (5.65)

Здесь

Для нахождения коэффициентов разложения  воспользуемся уравнением Шредингера в форме (5.56), в которой только отличны от нуля

                                      ,                       

(5.66)

.

Однородная алгебраическая система (5.66) имеет не тривиальное решения, если ее детерминант равен нулю, откуда

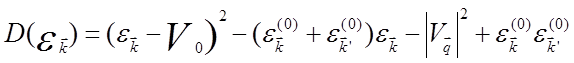        (5.67)

Отсюда находим поправки к энергии :

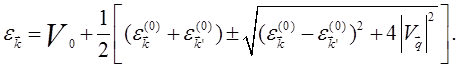                        (5.68)

Рассмотрим теперь для простоты одномерный случай. Введем величины 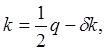 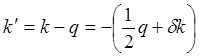.Тогда, поскольку , из (5.68) получаем

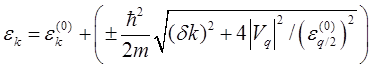.                              (5.69)

Или                     

 

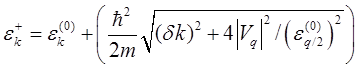
и

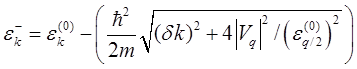.                                                             (5.70)

Из соотношения (5.69) видно, что вырожденный уровень энергии  (k=q/2) из-за воздействия возмущающего потенциала Vq расщепляется на два уровня:

 и .                                          (5.71)

Каждый из корней (5.70),  и.  соответствует вполне определенной

энергетической зоне: — первой (), — второй ().

Из (5.69) найдем поведение энергетических уровней вблизи границ зоны Бриллюэна. Однако, функцию следует рассматривать только при отрицательных , а функцию — только при положительных  (см. рис. 5.4, 5.5). Искажение вследствие возмущающего потенциала происходит, как уже отмечалось, не при всех , а лишь вблизи границы зоны Бриллюэна. Вдали от этой границы разность не является малой и может существенно превосходить .

Скачать файл