Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 18

Имеются предельные случаи, когда функции D_E(T), D_C(T) вычисляются явно. При  >> 1 (низкие температуры) [3]

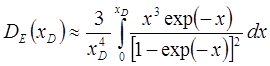                                                             (4.36)

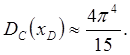                                                                   (4.37)

Тогда внутренняя энергия и теплоемкость кристалла

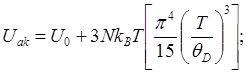                                                      (4.38)

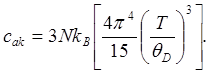                                                           (4.39)

Нетрудно видеть, что (4.38) и (4.30) совпадают с полученными ранее в разделе 4.2.1 формулами т.е. при низких температурах справедлив закон Дебая: с ~ Т ³. Подчеркнем, что закон ~Т ³ не связан с модельным подходом к вычислению теплоемкости, а лишь с зависимостью числа фононов от температуры (в трехмерном случае ~ Т ³).

При<< 1 (высокие температуры) [3]

                                                              (4.40)

                                                             (4.41)

откуда

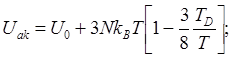                                                    (4.42)

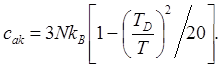                                                     (4.43)

Таким образом, и здесь, естественно, получаем закон Дюлонга-Пти (при << Т).

На рис. 4.4 представлена зависимость теплоемкости кристалла меди, . рассчитанная по формуле (4.35), точками нанесены экспериментальные значения теплоемкости. Из рис. 4.4 видно, что модель Дебая великолепно описывает данные эксперимента.

4.4. Уравнение состояния кристалла

Используя полученные в предыдущем разделе выражения для свободной энергии фононной подсистемы и известные термодинамические соотношения, построим уравнение состояния кристалла, учитывая то, что от объема системы явно зависит лишь частота Дебая.

.                                    (4.44)

При вычислении производной в (4.11) пользуются гипотезой Грюнайзена (E. Gruneisen), устанавливающей связь между частотой Дебая и объемом системы

,                                                        (4.45)

где – частота Дебая при некотором стандартном объеме ,– коэффициент Грюнайзена, являющийся также, как и частота Дебая характерным параметром кристалла.

Используя (4.45) из (4.44) для акустических фононов получим

. (4.46)

Уравнение состояния в форме (4.47) носит название уравнения Ми-Грюнайзена (G. Mie). Слагаемое – отражает вклад в давление нулевых колебаний, его часто объединяют с вкладом от статической части кристалла –

,                                     (4.47)

и используют следующее уравнение

.              (4.48)

Для P₀ используют следующее эмпирическое соотношение [?]

.                           (4.49)

Здесь  Па, , – эмпирические коэффициенты.

Аналогичным образом могут быть получены формулы для расчета коэффициента сжимаемости  и теплового расширения :                                                                                                                     

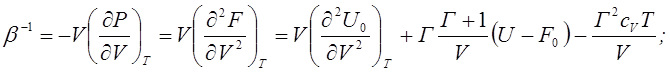  (4.50)

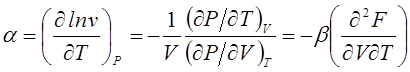.                                 (4.51)

Коэффициенты сжимаемости и теплового расширения, равно как и теплоемкость кристалла при постоянном объеме надежно определяются экспериментальным путем. Объединяя уравнения (4.50) и (4.51) получим уравнение для определения коэффициента Грюнайзена

.                                                 (4.52)

Можно определить коэффициент теплоемкости кристалла для каждой длины волны (волнового числа К) типа s

.                               (4.53)

Аналогично можно определить коэффициент Грюнайзена для каждой длины волны (волнового числа К) типа s следующим образом

.                                   (4.54)

Коэффициент Грюнайзена всего кристалла может быть получен из следующего соотношения

.                                          (4.55)

Используя полученное выражение для частоты Дебая  , можно получить другую удобную для определения коэффициента Грюнайзена формулу

.                                    (4.56)

Из (4.56) следует, что коэффициент Грюнайзена может быть отрицательным и слабо зависит от температуры.

Для случая кристаллов с потенциалом взаимодействия  и учете взаимодействия лишь с ближайшими соседями существует простое соотношение для определения коэффициента Грюнайзена [Ashkroft & Mermin p 136]