Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 11

Решение этой системы разыскиваем в виде

                   и₀(t) = C₁ ехр[iω(K)t], v₀(t) = C₁ ехр[iω(K)t].   ·                               (3.15)

Здесь C₁, C₂– неизвестные константы, а ω(K) – неизвестная частота колебаний. Подставляя (3.15) в (3.14) и сокращая общий множитель, получаем

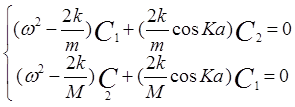                                      (3.16)

Соотношения (3.16) представляют собой систему однородных алгебраических уравнений относительно неизвестных константC₁, C_3. Не тривиальное решение системы (3.16) существует, если ее определитель равен нулю. В результате получаем дисперсионное уравнение для случая двух частиц в элементарной ячейке

D(ω, K)=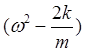 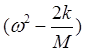-  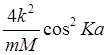= 0.                         (3.17)

Уравнение (3.17) имеет решения только при определенных частотах ω — корнях дисперсионного уравнения. Такие частоты называются собственными. Из (3.17) можно получить спектр собственных частот:

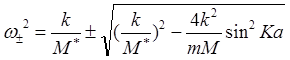                                 (3.18)

где М* = тМ/(т+М) — приведенная масса элементарной ячейки. Из (3.18) следует, что в сложной одномерной решетке, состоящей из атомов двух сортов, возникают две ветви колебаний: ω_- = ω_-(K) и ω₊ = ω₊(K). Исследуем свойства этих ветвей. Для Kа<<1 (в окрестности центра зоны Бриллюэна) имеем

, .

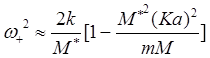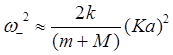Нетрудно видеть, что ветвь ω_-(K) есть ничто иное, как обычный звук (ср. с формулой (3.7) для колебаний простой решетки).

Поскольку элементарная ячейка имеет длину 2а, то соответствующая зона Бриллюэна имеет длину 2π/2а=π/а. Следовательно, достаточно рассмотреть в обратной решетке интервал волновых векторов

-π/2а ≤ K≤π/2а.                                          (3.19)

При Ka= π /2 (границы зоны Бриллюэна) имеем

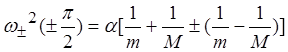
Можно показать, что на границах зоны Бриллюэна выполняются соотношения вида

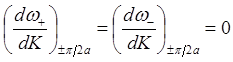
На рис. 3.4 показан ход двух найденных ветвей колебаний внутри зоны Бриллюэна (-π/2а, π/2а).

Изучим теперь характер колебаний отдельных атомов на различных ветвях спектра. Из (3.16) следует, что

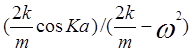 = .                                   (3.20)

Для Kа<<1 из (3.20) получаем

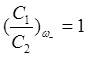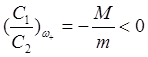,                                        (3.21)

Следовательно, для длинных волн на ветви  атомы движутся синхронно (в фазе): т.е., если u_n > 0, то и v_n > 0. На ветви  атомы движутся в противофазе (асинхронно): т.е., если u_n > 0, то v_n < 0. Причем для этой ветви выполняется соотношение

m u_n + M v_n = 0, т. е. их центр тяжести неподвижен. Если рассматривать случай коротких волн, когда , можно получить следующий результат: на ветви  неподвижными являются более легкие атомы, а колеблются более тяжелые, а на ветви — наоборот (показать). На рис. 3.5 представлена качественная картина колебаний атомов оптической и акустической ветвей.

Оценим ширину зоны  на ветви. Имеем

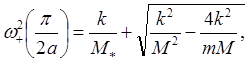                                             (3.22)

Отсюда в приближении m << М получаем (показать)

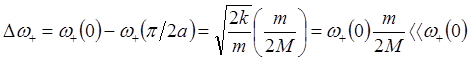           (3.23)

Из приведенного анализа следует, что колебания на ветви  при являются звуковыми волнами, поэтому эта ветвь носит название акустической, а ветвь — оптической.

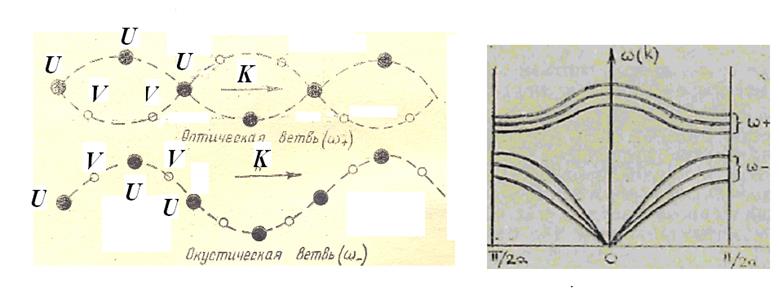                                    Рис. 3.5                                                   Рис. 3.6

Последнее связано с тем, что если в ячейке присутствуют разноименные ионы, то их колебания приводят к изменению электрического дипольного момента ячейки. Это в свою очередь ведет к оптической активности кристалла, т. е. к поглощению падающего на кристалл электромагнитного поля (это поглощение лежит в инфракрасном диапазоне, т е. в области частот ~10¹³ с^-1). С явлением оптической активности и вообще с оптикой кристаллов можно познакомиться в [1, 2, 6, 8].

В заключение отметим, что ветви  и  нигде внутри зоны Бриллюэна не пересекаются. Это означает, что элементарную ячейку сложной решетки можно рассматривать как некую «молекулу». В этом случае акустическая ветвь описывает фактически смещение такой «молекулы» как целого. Оптическая ветвь  характеризует тогда колебания атомов внутри «молекулы» - ячейки.

                          3.3. Колебания трехмерного кристалла