Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 21

Среднее число электронов в состоянии k  вычисляется  как

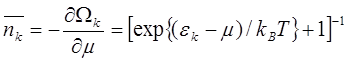                  (5.2)

Последнее соотношение носит название функции распределения Ферми— Дирака. Если имеется всего N₀ электронов, то должно выполняться условие нормировки

N₀ = 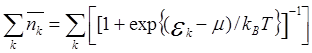 .                     (5.3

Уравнение (5.3) неявно определяет химический потенциал как функцию T и N₀. Для всей системы электронов, следовательно, термодинамический потенциал есть

Ω =                          (5.4)

Рассмотрим сначала электронную подсистему при нулевой температуре, предполагая, что электроны являются свободными частицами с волновыми функциями . Импульс и энергия выражаются в этом случае через волновой вектор :  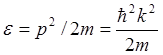. При нулевой температуре такая система называется полностью вырожденным ферми-газом. В силу специфических квантовых свойств электроны подчиняются принципу Паули по энергетическим уровням так, что их полная энергия минимальна, т.е. заполняют все энергетические состояния, начиная с минимальной энергии (равной нулю) до некоторой предельной, определяемой полным числом электронов N₀. Если имеется N элементарных ячеек в единице объема и на каждую приходится один атом, а число электронов в атоме равно z, то N₀ = Nz .

В силу того, что энергия зависит лишь от квадрата модуля импульса или квадрата модуля волнового числа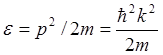, заполненные энергетические состояния представляют собой сферы в импульсном и волновом пространствах.

Подсчитаем число состояний, приходящееся на единицу объема V. Относительный объем, занимаемый одним электроном, равен (полный объем, приходящийся на один электрон, есть , следовательно, число электронов в слоях (р, р+dр), (k, k+dk) сфер заполнения в импульсном и волновом пространствах (с учетом того, что каждое состояние заполняют два электрона с антипараллельными спинами) определяются по формулам

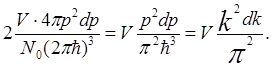                                          (5.5)

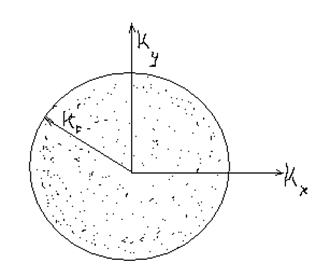
Рис.5.1

Электроны, как отмечалось выше, занимают при T=0 в импульсном и волновом пространствах все состояния от нуля до некоторого максимального значения p_F. Таким образом, общее число состояний, приходящееся на единицу объема (рис. 5.9), равно

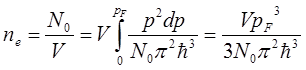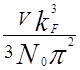=                  (5.6)

Отсюда находим граничные импульса, волнового числа и энергии:

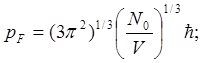
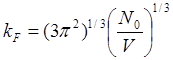 ;                         (5.7)

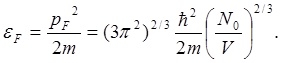                (5.8)

Величины p_F, k_F и  носят название соответственно фермиевского импульса, волнового числа Ферми и фермиевской энергии.

Энергия Ферми имеет простой смысл. Действительно, поскольку мы рассматриваем электроны в виде плоских волн, их спектр является непрерывным по , а следовательно, функцию распределения Ферми—Дирака (5.1) по энергиям можно записать в виде

                                       (5.9)

где —непрерывная функция импульса (и определенного значения спина). Из (5.9) видно, что при T=0 эта функция превращается в ступенчатую

 если ; если .                 (5.10)                                                                                                                                             

Последнее эквивалентно равенству . Это и есть определение энергии Ферми из статистики. Следовательно, в полностью вырожденном электронном газе химический потенциал совпадает с фермиевской энергией. Функция распределения  показана на рис. 5.10. Сделаем оценки величины  для типичных условий. Нетрудно видеть, что ~ а ^-2, где а — межатомное расстояние (поскольку /V, V~а^-3). Тогда . Найдем  Таким образом, длина волны электрона вблизи фермиевской сферы достигает межатомного расстояния. Следовательно, в кристалле электроны должны рассматриваться только в рамках квантовой механики.

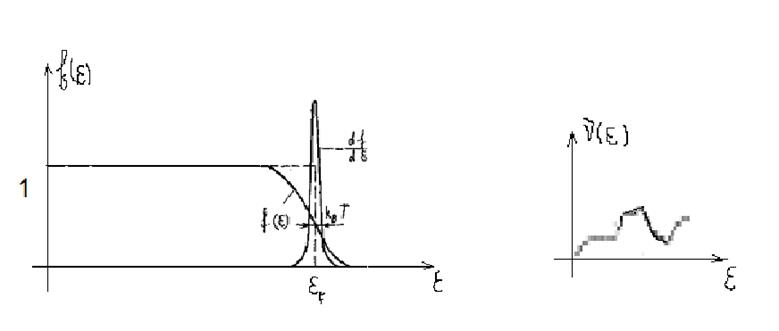
Рис.5.2                                                         Рис. 5.3

Отметим, что полная внутренняя энергия электронного газа U может быть найдена, если энергию в данном состоянии р²/2т (5.8) умножить на плотности состояний 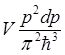 и затем проинтегрировать по сфере Ферми:

<E> 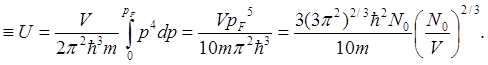            (5.11)