Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 7

На рис. 1.9.а показана зона Бриллюэна для ГЦК решетки (ей соответствует ячейка Вигнера—Зейтца для ОЦК решетки Бравэ). На рис. 1.9.б показана зона Бриллюэна ОЦК решетки (ей соответствует ГЦК решетка Бравэ с построенной ячейкой Вигнера—Зейтца).

Таким образом, введя понятие обратной решетки, нетрудно видеть, что любая физическая величина для периодической структуры, согласно (1.3), может быть разложена в ряд Фурье, где вектор пробегает все узлы обратной решетки.

Коэффициенты в (1.3) находятся из соотношения

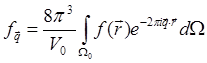                                                                               (1.11)

где — — объем элементарной ячейки обратной решетки.

Пространство, построенное па векторах , носит название — пространства. Заметим, что для —  пространства имеет место соотношение (ср. с формулой (1.11))

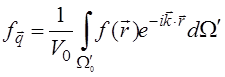                                                        (1.13)

где — объем ячейки в — пространстве.

Пользуясь полученными выше соотношениями, можно получить ряд полезных результатов для функций, описывающих свойства кристаллов [2, 6, 7].

1.2.3. Индексы Миллера

Индексы Миллера (W.H. Miller) используются для обозначения атомных плоскостей решетки. Любую плоскость можно однозначно задать точками пересечения этой плоскости с осями координат. Например, индексы Миллера для плоскости P , пересекающей оси координат в узлах решетки a, b, c с координатами (3,0,0), (0,6,0), (0,0,9), строятся так. Берутся векторы обратной решетки и координаты a, b, c в этих точках. Они будут равны 2π/3, 2π/6, 2π/9. Следовательно, эту плоскость можно характеризовать набором координат (2π/3, 2π/6, 2π/9) или набором значений (3, 2, 1), если привести координаты к общему знаменателю, который показывает величину сдвига в направлении каждого базисного вектора относительно начала координат.

Рис. 1.8а демонстрирует, как, зная пересечение данной плоскостью P. с осями координат в точках A, B. C,можно построить индексы Миллера. На рис. 1.8б приведено положение атомных плоскостей P, P₁, P₂. Им соответствуют индексы Миллера: плоскости P(1, -1,1)= (1, ,1), P₁ (0,-1,0)= (0, ,0), P₂ (1,0,0).

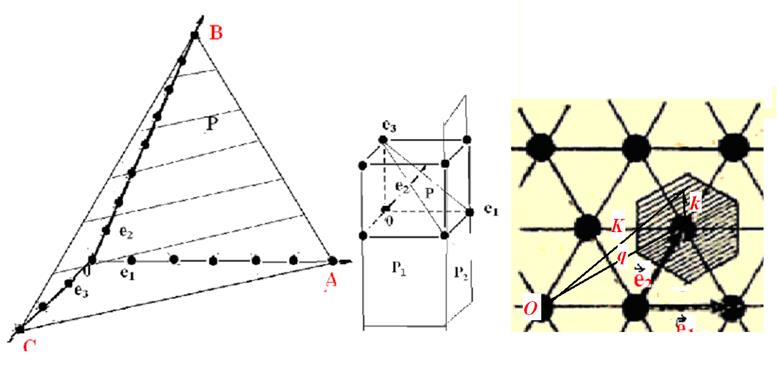
Рис. 1.10.а                     Рис.1.10.б                                   Рис.1.11.

1.2.4. Свойства волновых функций оператора Гамильтона в кристалле. Теорема Блоха

Энергию взаимодействия частиц, образующих кристалл, находят из решения уравнения Шредингера

(r) ‌ψ_K(r)> = ε_K‌ψ_K(r)>,                                 (1.14)

где (r) = -(ħ²/2m)Δ + V(r) – оператор Гамильтона, представляющей собой сумму операторов кинетической (здесь он записан в координатном представлении) и потенциальной энергии.

Рассмотрим, как изменяются волновые функции оператора Гамильтона ‌ψ_K(r)>, соответствующие значению энергии ε_K, при сдвиге ветора r на вектор трансляции прямой решеткиa. Исходя из физического смысла, полагают, что оператор Гамильтона при сдвиге на вектор трансляции решетки a не изменяется

(r+ a) = (r).                                                      (1.15)

Прежде чем ответить на вопрос об изменении волновых функций оператора Гамильтона ‌ψ_K(r)> при сдвиги вектора r на вектор трансляции прямой решеткиa , введем оператор сдвига на вектор трансляции решетки (a), который действует на любую функцию зависящую от координат f(r), включая и собственные функции ‌ψ_K(r)> оператора Гамильтона, от координат,(,?) следующим образом

(a) f(r)= f(r+a), (a) ‌ψ_Kr)> = ‌ψ_K(r+a)>.                         (1.16)

Покажем, что оператор трансляции является линейным оператором. Из определения (1.16) следует

(a) (С₁ ‌ψ₁(r)> + С₂ ‌ψ₂r)> = С₁ (a)‌ψ₁(r)> + С₂ (a) ‌ψ₂r)>.            (1.17)

Кроме того оператор трансляции (a) обладает следующим свойством (показать)

(a₁+a₂) = (a₁) (a₂).                                            (1.18)

Покажем, что оператор трансляции коммутирует с оператором Гамильтона, т.е. имеет место

(a)(r) = (r)(a).                                (1.19)

Использую определение (1.16) имеем

(a)((r) ‌ψ_K(r)> = (r + a) ‌ψ_K (r+a)> = (r) ‌ψ_K (r+a)>= (r) (a) ‌ψ_K(r)>, вычитая в этом равенстве из первого члена последний, получим