Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 20

Формула, связывающая f_a с другими параметрами конденсированного вещества:

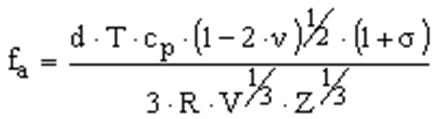, (2)

 где Z- число межатомного взаимодействия, V- объем одного киломоль вещества, c_p- решеточная теплоемкость при постоянном давлении одного киломоль вещества, R- универсальная газовая постоянная.

5. ЭЛЕКТРОННАЯ ПОДСИСТЕМА ТВЕРДОГО ТЕЛА

Влиянием электронов на физические свойства кристаллических твердых тел во всем предыдущем рассмотрении пренебрегалось. Однако, как будет видно из дальнейшего, свойства электронов в твердом теле существенно отличаются от свойств свободных электронов, поэтому такое рассмотрение необходимо. Эти отличия, кроме того, определяют в значительной мере характер различных явлений в кристаллах, в частности кинетических, и позволяют определить, является ли данный кристалл диэлектриком, полупроводником, металлом или полуметаллом. Помимо кинетики электронов в кристаллах, которая будет изучена в дальнейшем, электронная подсистема вносит специфический вклад в термодинамику. Этот вопрос будет обсуждаться ниже.

Электроны в твердом теле, в отличие от рассмотренных выше колебаний атомов решетки, следует описывать квантовомеханически, поскольку характерная длина их волн де Бройля в пределах межатомного расстояния  (это неравенство будет доказано ниже).

Современные представления о твердом теле позволяют выделить две группы электронов: свободные и связанные (локализованные). Первые возникают в твердом теле за счет перекрытия волновых функций отдельных атомов при их сближении. Вторые представляют собой электроны внутренних оболочек, локализованные около «своих» атомов. Валентные электроны изолированных атомов при образовании твердого тела становятся, как правило, свободными, т. е. способными перемещаться по всему кристаллу.

При рассмотрении поведения электронов в кристалле обычно используют два важных предположения. Первое заключается в пренебрежении влиянием движения атомов на энергетический спектр электронов. Возможность такого подхода связана с существенным различием скоростей атомов и электронов в твердом теле. Отношение скоростей атомов и электронов предстает в виде , где c, М, v_e, m — соответственно скорости и массы атомов и электронов. При выполнении такого неравенства движение электронов определяется мгновенным положением ионов (атомов), а медленное движение ионов происходит под действием лишь среднего пространственного распределения электронов. Такое приближение носит название адиабатического. Суть такого названия состоит в том, что электроны адиабатически следуют за движением ионов, поэтому можно считать, что электроны находятся просто в заданном потенциальном поле ионов. Если учитывать влияние движения ионов на энергетический спектр электронов, то придем к электрон—фотонному взаимодействию. В дальнейшем, однако, мы его не учитываем.

Второе предположение при построении энергетического спектра электронов в твердом теле состоит в пренебрежении взаимодействием электронов друг с другом. Существуют способы, с помощью которых многоэлектронную задачу удается свести к многоэлектронной. Одним из таких методов, например, является метод Хартри—Фока, основная идея которого состоит в замене потенциальной энергий электронов 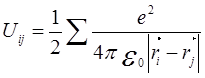 некоторым эффективным потенциалом — внешним полем , в котором каждый электрон движется независимо, но в эффективном потенциальном поле, создаваемым всеми остальными зарядами. Такое предположение позволяет описывать любой электрон индивидуальной волновой функцией. Последнее обстоятельство существенно упрощает рассмотрение энергетического спектра электронов в кристалле

5.1. Статистика электронов и плотность электронных состояний в кристаллах

Рассмотрим сначала статистические и термодинамические свойства электронов в кристаллах не учитывая их взаимодействие с потенциальным периодическим полем ионов.

Электроны обладают полуцелым спином. Частицы c полуцелым спином являются фермионами и подчиняются квантовой статистике Ферми— Дирака. Термодинамический потенциал электронов в k-ом состоянии есть [10]

                                       (5.1)