Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 23

Теперь обратимся к вычислению названных интегралов. Нетрудно видеть, что эти интегралы можно записать и форме

J = 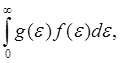                                                     (5.17)           

где — некоторая произвольная функция энергии. Проинтегрируем (5.17) по частям:

J = 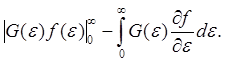                                            (5.18)

Здесь  = g(ε), .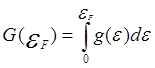

Видно, что в (5.18) первый член обращается в нуль, т.к. g(0)=0 и G(ε) g(ε) → 0 при ε →∞. Второй член в (5.18) может быть вычислен благодаря следующему обстоятельству. Как отмечено выше, в металлах . Поэтому при T ≠ 0 функция дf/дε имеет симметричный пик пиком шириной ~ при (см. рис. 5.2), а при T = 0 ведет себя как δ-функция δ(ε - ). При этом G можно разложить в ряд Тейлора вблизи :

  

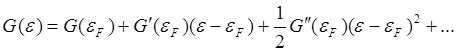
и представить интеграл J в виде ряда

J = - =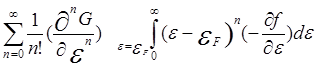

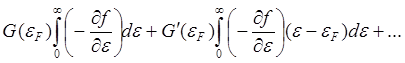=-                                (5.19)

Входящие в J  интегралы можно привести к безразмерному виду

 ==

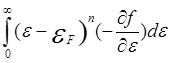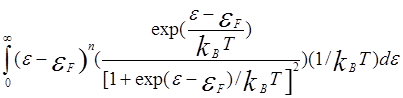= (k_BT)ⁿ = .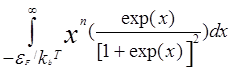

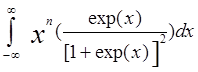Поскольку ε_F/k_BT >> 0 и I_n ≈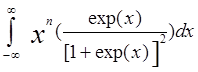, интеграл (5.19) можно представить в виде ряда

J =- 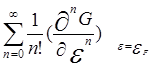(k_BT)ⁿ I_n, I_n =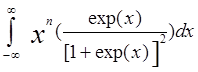

Для четных n подынтегральная функция антисимметрична и эти интегралы равны нулю I_2n-1 = 0. Используя это представление для интеграла I_2n , получим

I₀ = 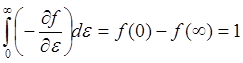, I_2n≠ 0, n = 0, 1, 2.   , I₂ = π²/5.                 (5.20)

Из (5.89) следует

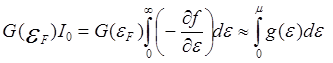.                                            (5.21)

(1/2)I₂ =(1/2)I₂ =()_εF 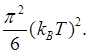                                  (5.22)

Следовательно, для любой функции от энергии g(ε) с точностью до отношения (k_BT/ε_F)²<< 1, получаем

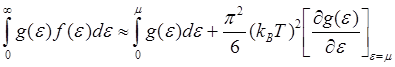+ O((k_BT)⁴).                       (5.23)

Воспользуемся этим методом для расчета всех термодинамических функций.  Сначала рассмотрим зависимость химического потенциала от температуры, т.е. зависимость μ(Т). Число электронных состояний, с использованием (5.22) можно записать как

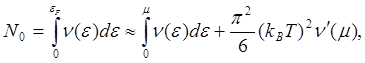                        (5.24)

где , (T) - зависящая от температуры добавка к химическому потенциалу электронов при T = 0, равному  

Учтем, что число электронов в кристалле N₀ не зависит от T и равно:

                                     

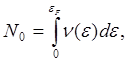
Тогда, преобразуя (5.24), получаем  N₀ =  =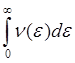

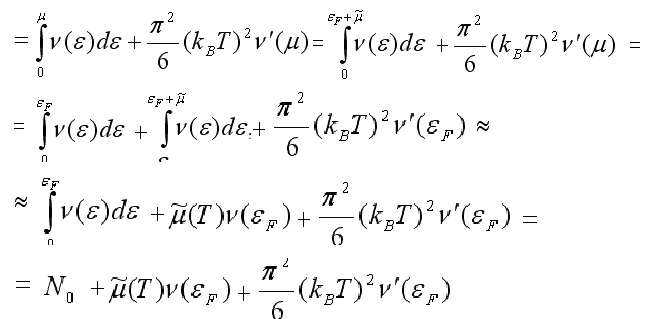 (5.25)

Из (5.25) получаем зависящую от температуры добавку к химическому потенциалу (T),

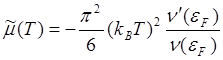.                              (5.26)

Оценим ее отношение к химическому потенциалу электронов при T = 0, равному , поскольку ν()~^1/2, ~.

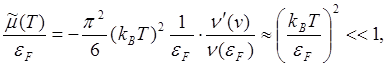       (5.27)

Окончательно зависимость химического потенциала от температуры имеет вид

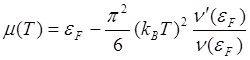,=                           (5.28)

Вычислим внутреннюю энергию электронов при T ≠ 0, используя соотношение (5.22):

=

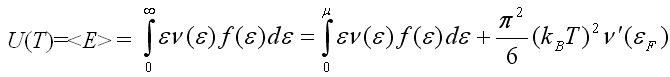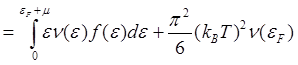 .                                       (5.29)

Зависимость внутренней энергии электронов от температуры имеет вид 

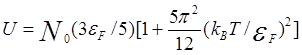.                                             (5.30)

Теплоемкость при постоянном объеме равна

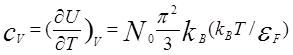.                                                (5.31)

Обсудим получившееся выражение для теплоемкости электронов в кристалле. Физический смысл полученного соотношения ясен — только электроны вблизи энергии Ферми могут принимать участие в тепловом возбуждении системы. Число таких электронов, как говорилось выше, порядка , умноженное на плотность состояний вблизи . Каждый электрон вносит в (5.102) вклад . Важно отметить, что при получении (5. 102) нам не нужны были никакие данные о функции плотности состояний . Следовательно, теплоемкость для всех металлов является линейной функцией температуры. Понятно также, что при малых температурах основной вклад в теплоемкость твердого тела дают электроны, поскольку c_Ve~ Т, а для решеточной теплоемкости c_Vp~ Т^5.

Рассмотрим теперь соотношение между c_Ve и c_Vpпри высоких температурах (Т>Θ_D). Получим сначала для оценок формулу теплоемкости для газа свободных электронов. В этом случае, как нетрудно показать, химический потенциал мало отличается от энергии Ферми

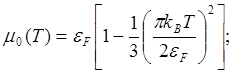 ≈.                                        Теплоемкость электронной подсистемы растет линейно

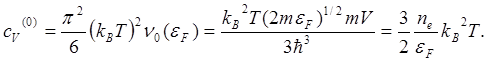              (5.32)

Подставив в (5.32) характерные значения п_eи  (например при п_e ~10²² см^-3, 7 эВ, T~0.03 эВ), получим

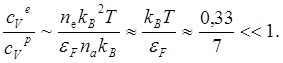                                  (5.33)