В этом случае иkпредставляют собой так называемые нормальные координаты, в которых уравнения вида (3.5) для разных n становятся независимыми. Действительно, подставляя (3.6) в (3.4), приходим к обыкновенному дифференциальному уравнению для функции и0(t)
= 
.
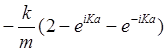(3.6)
Будем искать решение в виде
и0(t) = C ехр[iω(K)t]. · (3.5)
где C– неизвестная константа, ω(K) – частота колебаний. Подставив (3.5) в (3.6), приходим к дисперсионному уравнению, устанавливающему связь между частотой колебаний ω(K) и волновым числом K
=
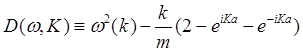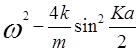= 0. (3.6)
.
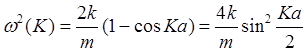Решая уравнение (3.6) находим частоту колебаний
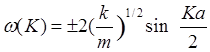(3.7) или
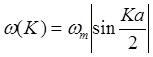
где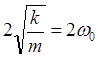 
. Колебания
кристалла в рассматриваемой модели представлены в виде совокупности независимых гармонических осцилляторов, каждый со своей частотой 
. Соотношение 
носит название закона дисперсии.
Согласно (1.28)
вектор обратной решеткиK изменяется в пределах зоны Бриллюэна и для одномерного
случая имеем
-π/а ≤ K ≤π/а// (3.8)
Изменения смещений атомов решетки от положения равновесия аналогично колебаниями непрерывной струны и решение уравнений (3.2) соответствует плоской волны:
ип(t) = C ехр[i(ω(K) t + iKan]. (3.9)
Зависимость частоты колебаний (3.7) на в пределах зоны Бриллюэна –
на интервале -π/а ≤ 
≤ π/а, показана на рис. 3.3.
Проанализируем соотношение (3.7). При Kа<<1 (длинные волны), имеем
ω = ω0Ka =cK (3.10)
где с =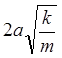 
=
= 
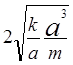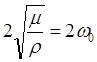– скорость звука, μ = k/a– модуль упругости материала, ρ
= m/a3–
плотность. Фазовая скорость волн
Vf = 
= c. (3.11)
Следовательно, при малых K рассмотренные колебания решетки являются
обычным звуком. Дисперсия отсутствует, т. е. все длинны волн (разные
K) движутся с
одной скоростью, поэтому показанную на рис. 3.2 зависимость
называют акустической ветвью. При
Kа~π, ω~2ω0 ,
т. е. все атомы колеблются с одной частотой 2ω0.
В общем же случае дискретная среда обладает дисперсией,
т. е. зависимостью фазовой скорости распространения Vf = от длины волны λ (от
волнового вектора K =
2π/λ).
Для с~5103м/с, а~10-8 см из (3.10) получаем 2ω0~5-1013 с-1. Отметим, что независимое измерение скорости звука в твердых телах может дать величину упругой постоянной k, модуль упругости μ = k/а. Действительно, для приведенных выше параметров и ρ = 8 г/см3, μ=k/а ≈ ρс2 ≈ 2 1011 Н/м3.
3.3. Колебания в одномерной цепочке (случай двух частиц в ячейке)
Выше были рассмотрены колебания цепочки частиц в случае, когда в ячейке находился лишь один атом. Это соответствует колебаниям простой решетки. Для многих кристаллов
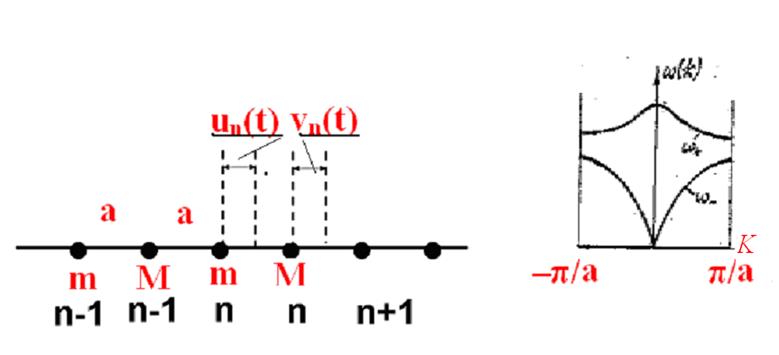Рис.
3.3 Рис. 3.4
в элементарной ячейке имеется больше одного атома (например, алмазе, NаС1, Gе и т. п.). Рассмотрим теперь колебания такой сложной решетки, у которой два атома в элементарной ячейке (рис. 3.3). Для простоты будем полагать, что между всеми атомами расстояние одинаково и равно а, аналогично одинаковы и упругие постоянные всех атомов k, а массы атомов равны соответственно m и М. Тогда по аналогии с (3.4), ограничиваясь лишь взаимодействием с ближайшим соседом, имеем
= — k(un—v n-1,) - k(un— vn)
(3.12)
= — k(vn — un,) - k (vm— un+1,).
Так же, как и в случае колебаний простой решетки, ищем решение системы уравнений в виде плоской волны
, 
,
(3.13)
где u0(t), v0(t) – неизвестные функции времени.
Подставив (3.13) в (3.12) и сократив на общий множитель, приходим к системе обыкновенных дифференциальных уравнений для функций u0(t), v0(t)
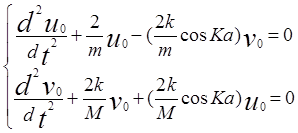(3.14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.