Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 16

Как уже отмечалось, фононы подчиняются квантовой статистике Бозе-Эйнштейна, поскольку в каждом состоянии может находиться произвольное их число. На классическом языке это соответствует волнам произвольной амплитуды, распространяющимся в решетке. Понятно, что если в кристалле возбуждено большое число фононов, то их совокупность можно описывать статистически.

Описание колебаний решетки в терминах полностью независимых фононов возможно, если оставить в разложении потенциальной энергии взаимодействующих атомов только члены, квадратичные по смещениям из положения равновесия. Если удержать члены более высокого порядка, то появляется фонон—фононное взаимодействие (оно вызывает рассеяние фононов с различными импульсами (различными ) друг на друге, приводя к конечному времени их жизни, а также к смещению энергии отдельного фонона [2, 6, 7]). Другим видом взаимодействия, влияющим на динамику фононов, является электрон-фононное взаимодействие, появляющиеся при учете взаимного влияния ионов и электронной подсистемы. Указанные взаимодействия приводят к установлению теплового равновесного движения в решетке [2,6,8]. Эти процессы рассматриваются в кинетике.

4.2. Статистика и плотность состояний фононов

Рассмотрим более детально получение плотности состояний фонов  — числа фононов на интервал частот. Поскольку число состояний фиксировано числом степеней свободы, то получим условие нормировки

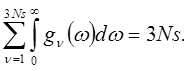                                       (4.6)

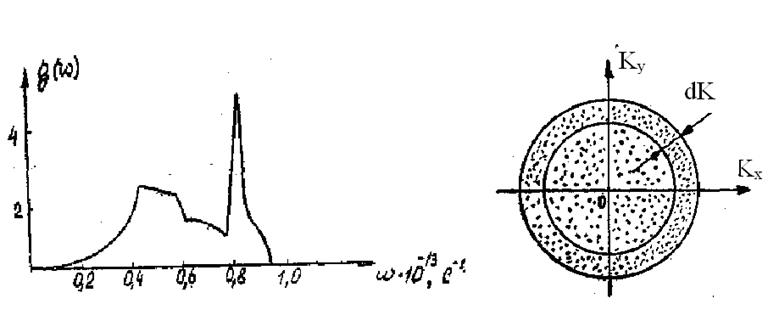
Рис. 4.1                                                   Рис. 4.2

Выражение (4.3) с учетом (4.6) можно записать в виде

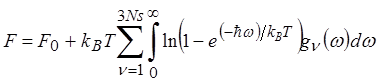                             (4.7)

Здесь суммирование производится по всем 3s ветвям спектра, а интегрирование по всем частотам. Введение функции плотности состояний позволяет использовать ее вместо плохо известного, как правило, закона дисперсии . Хотя плотность состояний для реального кристалла — также весьма сложная функция, она может быть получена из эксперимента. Например, для А1 поведение показано на рис. 4.1 Понятно, что использовать функцию  такого сложного  вида для расчета термодинамических характеристик практически невозможно. Однако существуют физически ясные схемы упрощения вида , которые ниже будут приведены и использованы.

Для вычисления (4.7) и ряда других термодинамических функций, связанных с фононами, необходимо, как уже отмечалось, знание функций . Рассмотрим некоторые предельные случаи, когда  можно вычислить в явном виде.

4.2.1. Случай низких температур

При низких температурах возбуждаются фотоны акустической ветви с энергией, пропорциональной волновому вектору:

                                                     (4.8)

( = 1, 2, 3 — три акустических ветви). Оценим  . Пусть ~5 см/с, ~0,1 (а — межатомное расстояние), тогда ~10^-15 эрг или  ~10 К.

Таким образом, рассматриваемый случай низких температур соответствует . В кристалле имеется три типа звуковых колебаний (соответственно три типа фононов): продольные, со скоростью и поперечные, со скоростью . Функцию в этом случае можно записать в виде .

Вычислим функции  и . Для этого найдем число собственных колебаний в спектре звуковых волн с абсолютными значениями в интервале (рис. 4.3). Минимальный объем, приходящийся на одно значение , равен (V — объем тела). Следовательно, число колебаний  в равно

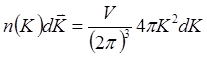                                         (4.9)

Но для звука  , откуда получаем

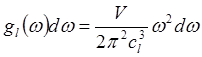                                         (4.10)

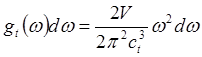.                                  (4.11)

Двойка в числителе (4.11) отражает два типа поляризации поперечных волн. Таким образом, получаем

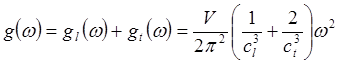                          (4.12)

Обычно вводят некоторую среднюю скорость согласно формуле

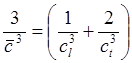                                        (4.13)

Тогда (4.12) принимает вид

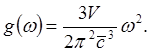                                        (4.14)

Подставляя (4.12) в (4.7) и учитывая, что  = 1, 2, 3, получаем формулу для свободной энергии

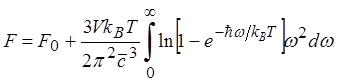                                 (4.15)

Здесь верхний предел ограничен не величиной , а принят бесконечным, поскольку очевидно, что при низких температурах большие  вклад в интеграл не дают. Если ввести, то интеграл (4.15) интегрированием по частям сводится к стандартному виду (показать)