Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 31

Поясним механизм возникновения сплошного спектра электрона внутри разрешенной зоны при объединении в решетку отдельных атомов, имеющих дискретный спектр. Начнем со случая соединения двух атомов. Пусть два изолированных атома находятся в основном состоянии с волновыми функциями и . Система из двух изолированных атомов двукратно вырождена: одному значению энергии соответствуют две волновые функции. При соединении атомов волновые функции  и  перекрываются и существует уже два состояния (два уровня энергии, образующиеся перекрытием волновых функций). Таким образом, двукратное вырождение снимается.

В случае соединения в решетку N атомов все происходит аналогично (рис. 5.12b). Система N изолированных атомов в основном состоянии является N-кратно вырожденной (одному значению энергии соответствует набор функций {, , …,}. При сближении атомов вырождение снимается за счет расщепления каждого уровня на N состояний (например, 3s — состоянию изолированных атомов соответствует 3s— зона из N состояний и т. д.). Таким образам, возникает зона состояний с очень близкими энергиями. При большом N эти состояния располагаются практически непрерывно, образуя зону разрешенных значений энергии. Важно отметить, что в принципе возможен случай, когда две или несколько зон перекрываются из-за значительного их расширения (см. рис. 5.12b). В этом случае метод построения волновых функций несколько изменяется (см. подробнее, например, [2, 6]). Явление перекрытия зон имеет большое значение в целом ряде эффектов и существенную роль играет при определении типа твердого тела.

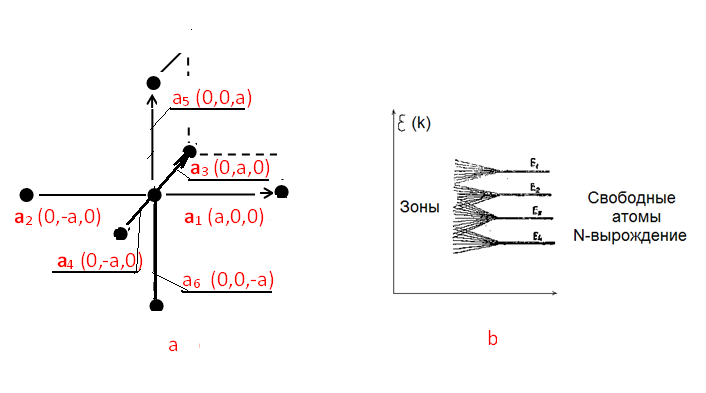
Рис. 5.12

5.4. Вклад взаимодействий электронов в термодинамические функции

В общем случае, кроме взаимодействия электронов с ионами решетки, необходимо учесть и кулоновское взаимодействие электронов между собой.

В этом случае уравнение Шрёдингера для электронов (5.86) будет иметь вид

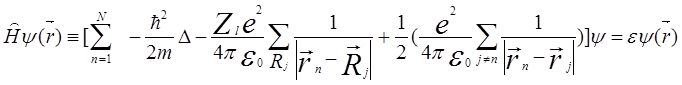. (5.98)

Здесь

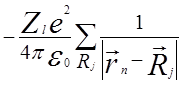 - взаимодействие электронов с ядрами атомов, находящихся в узлах решетки Бравэ, - число электронов находящихся на связанных с ионом уровнях;

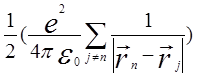-  кулоновское взаимодействие электронов между собой.

Учет изменения энергии свободных электронов за счет из взаимодействия с решеткой в приближении слабой связи был разобран в разд.5.5.2 , где была получена формула для волновых чисел, не принадлежащих границам зоны Бриллюэна (5.63)

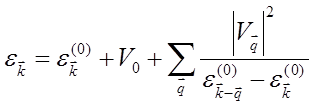
Можно ограничиться лишь первой добавкой V_0, связанной с изменением уровня отсчета энергии, однако, следовало бы учесть, экранирование ионного состава свободными электронами, что приводит к отличию потенциала взаимодействия φ(r) от кулоновского φ_c(r) = eZ_l/rε₀.

Задачу об экранировании разберем в приближении Томаса-Ферми, записав уравнение Пуассона в виде 

n₀]/ε_0.                                       (5.99)

Для определения воспользуемся тем, что для свободных электронов их химический потенциал зависит от концентрации электронов

μ₀=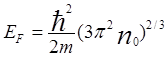

В той области кристалла, где возникает нарушение электронейтральности, локальный химический потенциал можно записать в виде

μ= 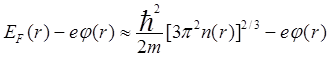.                   (5.100)

Поскольку число электронов не изменяется, то и при нарушении электронейтральности должно выполняться условие

μ₀= 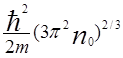=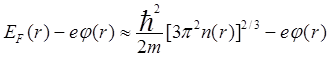,       которое можно представить в виде

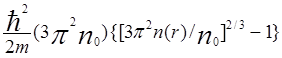= . (5.101)

Разлагая (5.101) в ряд Тейлора находим, что разность n(r) - n₀ можно представить в виде

, или

.                           (5.102)

Уравнение (5.99) принимает вид

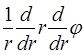 =                                    (5.103)

Решая это уравнение с граничными условиями

φ(r) → 0 при r → ∞ и φ(r) → φ_c(r) = eZ_l/4πrε₀ при r → 0,          (5.104)

представим экранированный потенциал в виде

φ(r) = eZ_l exp(-λr)/ 4π rε₀ ,                                                         (5.105)

где            λ = 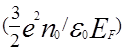^-1/2.                                                                       (5.106)

1/λ = 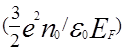^1/2 – длина экранирования.

Теперь периодический потенциал взаимодействия электронов с ионами в решетке V(x) = V(x + a) можно представить в виде

V(x) = - e²Z_l exp(-λx)/4π xε₀ при 0 ≤ x ≤ a/2

И