Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 12

Модели колебаний кристалла, рассмотренные выше, показывают основные закономерности, возникающие при этом. Представляет несомненный интерес рассмотреть колебания трехмерного кристалла. Однако математическая теория таких колебаний выглядит очень сложно, хотя результаты получаются достаточно ясными. В этой связи ограничимся здесь лишь постановкой задачи и качественными соображениями.

Понятно, что колебания трехмерного кристалла должны описываться некоторой векторной функцией — смещением атомов из положения равновесия в точке . Функция  должна зависеть от номера ячейки и номера атома в данной ячейке. Таким образом, колебания трехмерного кристалла описываются функцией , где индекс  обозначает номер ячейки, а — номер атома в этой ячейке. Возникающие в данном случае уравнения движения аналогичны рассмотренным ранее для одномерной цепочки. Решение этих уравнений можно опять искать в виде плоских волн (для заданной ячейки)

                                 (3.24)

Здесь представляет собой амплитуду колебаний, которая  различна для разных  атомов данной ячейки. Векторы определяют не только  амплитуду  колебаний, но и их поляризацию (т. е. направление колебаний в волне по отношению к волновому вектору ). Подстановка (3.24) в уравнения движения дает по аналогии с одномерным случаемдисперсионное уравнение , определяющее спектр колебаний трехмерного кристалла. Можно показать (см., например, [11]), что если в ячейке содержится s атомов (т.е. j = 1, 2,. . ., s), то число колебаний, определяемых дисперсионным уравнением, есть 3s. Таким образом, при заданном  имеется 3s частот (3s ветвей колебаний). Напомним, что в одномерной цепочке имеется s ветвей колебаний: в простых решетках (s = 1) — одна акустическая ветвь, в сложных, с двумя атомами на элементарную ячейку (s = 2)—две ветви: акустическая и оптическая.

Оказывается, что и в трехмерном случае все колебания распадаются на акустические и оптические ветви. Рассмотрим сначала колебания простой трехмерной решетки (с одним атомом на ячейку). Ясно, что при малых  (длинные волны) атомы совершают колебания с частотой , стремящейся к нулю вместе с  = 0. Эти колебания являются, очевидно, звуковыми. При  такие колебания переходят в простое параллельное смещение всей решетки. Звуковых воли в данном случае три в соответствии с тремя типами поляризации.

Если , то смещения обозначаются , и колебания носят название поперечных, а если ,—продольных (обозначается ). При малых  справедливо, как и для звуковых воли в одномерной цепочке, соотношение

                       (3.25)

где индекс i соответствует трем акустическим  ветвям, — не зависят от модуля вектора , а лишь от его направления. Таким образом, существует три скорости звука в кристалле: две поперечные, (одинаковые) и равные и одна продольная, равная . Приведем оценки этих скоростей, например, для молекулярных кристаллов инертных газов: Nесм/с; см/с; Ar см/с; см/с.

Отмстим, что в длинноволновом приближении получаются уравнения сплошной среды (уравнения теории упругости), если характерные длины волн много больше постоянной решетки. Например, в случае малых деформаций сплошной упругой среды (свойства которой предполагаются, кроме того, не зависящими от направления) для плоских упругих волн, в которых зависит лишь от одной координаты, например x, получаются уравнения:

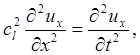
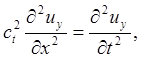
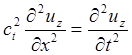                        (3.26)                                                                       

Известно, что между  и  выполняется соотношение >. В теории упругости и выражаются через упругие постоянные среды и плотность:

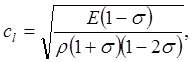
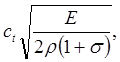                                       (3.27)

где Е — модуль Юнга, — коэффициент Пуассона, — плотность среды — хорошо известные из опыта величины.

Если вернуться к колебаниям сложной трехмерной решетки, то оставшиеся после выделения трех акустических ветвей (3s—3) ветви колебаний характеризуются тем, что при  = 0 частоты  не обращаются в нуль. Таким свойством, как показано выше, обладает оптическая ветвь (в одномерном случае). Следовательно, оставшиеся (3s—3) ветви являются оптическими.