Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 14

Отсюда находим средние числа заполнения  (или функция распределения по состояниям)состояний :

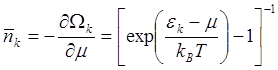               (3.32)

Выражение (3.32) представляет собой функцию распределения идеального газа, подчиняющегося статистике Бозе-Эйнштейна (или, как говорят, бозе-газа). Термодинамический потенциал бозе-газа в целом получается суммированием по всем состояниям:

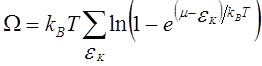.                      (3.33)

Применяя статистику Бозе-Эйнштейна к фононам, следует учесть, что их число не сохраняется, а должно определяться из условий термодинамического равновесия системы. Как известно из термодинамики [11], последнее должно состоять в минимальности свободной энергии (при заданной температуре Т и объеме V) по отношению к числу частиц в системе:. С другой стороны,  и, следовательно, = 0. Таким образом, для системы с переменным числом частиц (например, как и для газа фотонов) химический потенциал равен нулю. Поскольку , из = 0 следует . Отсюда для фотонов (при постоянных Т, V) свободная энергия и термодинамический потенциал совпадают.

                                            (3.34)

Для чисел заполнения  имеем

 .                             (3.35)

Распределение по частотам колебаний (3.35) для фотонов называется распределением Планка. Из (3.35) нетрудно получить число фотонов при  >>

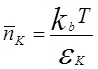                            (3.36)

Таким образом, число фононов в состоянии пропорционально температуре (при Т>>).

Вернемся снова к колебаниям частиц в решетке кристалла. С точки зрения квантовой механики волна с частотой ω_-(K) представляет собой квантовый гармонический осциллятор. Уравнения Шрёдингера для гармонического осциллятора с частотой w(K) имеет вид

,

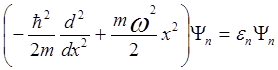Его собственные функции и собственные значения хорошо известны []

,                                          (3.37)

где – целые числа.

Зная собственные значения энергии (3.38), для гармонического осциллятора можно найти статистическую сумму

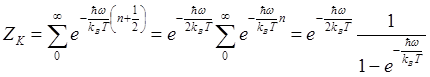.                    (3.38)

Теперь, зная статистическую сумму, найдем выражение для термодинамического потенциала:

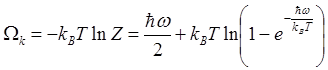.                                    (3.39)

Поскольку фононы (волны) представляют собой систему с переменным числом частиц, то для нее в состоянии равновесия химический потенциал равен нулю μ = 0 [] и следовательно термодинамический потенциал и свободная энергия совпадают

.                                                            (3.40)

Зная статистическую сумму, можно найти внутреннюю энергию -ого состояния воспользовавшись известным соотношением статистической физики [].

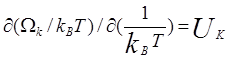.                                       (3.41)

Используя (3.39) и  (3.41) для внутренней энергии  -ого состояния получаем

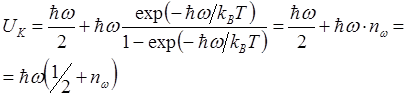                       .(3.42)

В формуле (3.42) использовано соотношение для числа частиц, находящееся  в данном состоянии, которое согласно сказанному выше, находится так

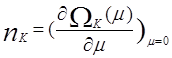= .                                         (3.43)

Полученная здесь функция распределения частиц по энергиям – по частотам , хорошо известна в статистической физики и, как отмечено выше , она соответствует квантовым частицам с целым спином (базонам) и носит названия функции распределения Бозе−Эйнштейна

Из формул (3.42), (3.43) видно, что каждую отдельную волну, в которой участвуют все атомы решетки, с волновым вектором и и соответствующей ему частотой можно трактовать как квазичастицу. В данном случае такая квазичастица получила название  фонона. Фонон обладает импульсом =  и энергией=. Из (3.43) следует, что полное число фононов  в -ом состоянии (при данной частоте) зависит только от  температуры.

Отметим еще раз основные свойства фононов. Во-первых, фононы подчиняются статистике Бозе-Эйнштейна (они имеют целый спин). Во-вторых, энергия фононов и импульс формально такие же, как и у обычных частиц. Однако  не является обыкновенным импульсом. Импульс, например, электрона (в вакууме) может сохраняться при столкновениях. Импульс же фонона сохраняется лишь с точностью до произвольного вектора обратной решетки:

,                                                  (3.44)