Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 22

В общем случае электронной подсистемы, находящейся при ненулевой температуре в кристалле, для построения ее термодинамики необходимо знание электронного энергетического спектра, как это видно из (5.2), (5.11). Энергетический спектр электронов в кристалле является фактически непрерывным. В этом случае удобно перейти от сумм в (5.3), (5.4) к интегралам, введя функцию плотности электронных состояний. Аналогично тому, как это делалось при рассмотрении тепловых свойств решетки, введя функцию плотности состояний фононов g(ω) Аналогично и для электронов можно воспользоваться общей формулой перехода от сумм к интегралам с функцией плотности энергетических состояний электронов, которую здесь будем обозначать как ν(ε). Интегрирование будет распространяется на всю область энергий свободных электронов (для последующего изложения с учетом зонной теории, отметим, что в запрещенных зонах ν(ε)=0).

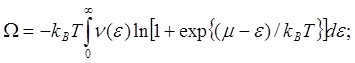          (5.12)

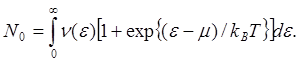                           (5.13)

Здесь функция плотности энергетических состояний электронов ν(ε) дает число состояний на интервал энергии d. Аналогично для внутренней энергии для электронной системы получим

U =<E> = =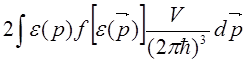        

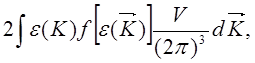
где — плотность состояний в пространстве квазиимпульсов,  — плотность состояний в волновом пространстве, к формуле интегрирования по всем значениям энергии свободных электронов

<E> = 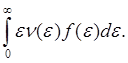                                     (5.14)

Итак, из формул (5.12) — (5.14) видно, что для определения термодинамических функций электронов необходимо знание плотности состояний ν(ε). Отметим, что в реальных кристаллах функция ν(ε) имеет весьма сложную структуру, например, как на рис. 5.11. Это связано со структурой зоны Бриллюэна в кристалле.

Интегралы (5.12)—(5.14), вычисление которых необходимо для нахождения термодинамических функций, со столь сложной функцией ν(ε). не удается рассчитать аналитически. Существуют случаи, когда ν(ε) можно упростить и получить необходимые результаты в аналитическом виде. Например, для свободного электронного газа, когда поверхность постоянной энергии в волновом пространстве и пространстве импульсов -  формула (5.5), позволяет достаточно просто определить число состояний и в энергетическом пространстве:

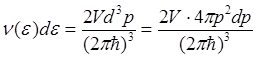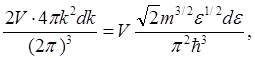=                            (5.15)

Формула (5.15) дает число состояний в интервале , откуда для единицы объема V=1 получаем

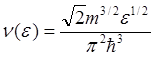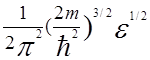= .                     (5.16)

Как будет показано далее, явный вид плотности состояний и в общем случае выглядит аналогичным образом (например, для электронов вблизи экстремумов зон Бриллюэна, где они ведут себя почти как свободные, но с эффективной массой , отличной от т). Закон дисперсии электронов – зависимости энергии от импульса или волнового числа, в этом случае есть и выражение (5.16) заменяется на

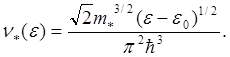
Ниже будут рассмотрены конкретные примеры выбора функции плотности состояний для вычисления термодинамических величин в металлах и полупроводниках.

5.2. Термодинамика свободных электронов в металлах

Рассмотрим случай металла, для которого справедливы следующие рассуждения. Разрешенные энергетические зоны металла являются неполностью заполненными. Поэтому при нагреве металла электроны могут переходить в ближайшие энергетические состояния внутри разрешенной зоны. С другой стороны, по причине заполнения состояний с учетом принципа Паули только те электроны могут получить энергию k_BТ (при температуре Т), которые находятся на расстоянии ~ k_BТ от уровня энергии Ферми . Таким образом, только самые близкие к уровню Ферми электроны дают вклад в термодинамические свойства. Из этих рассуждений следует, что поскольку для разумных температур Т<Т_т ( — температура плавления) выполняется соотношение , то электроны в металле являются всегда вырожденными. Если ввести температуру вырождения  то всегда для металлов выполняется условие T<<Т₀. Следовательно, электроны в металле представляют типичный случай вырожденного ферми-газа. В силу сказанного для металлов интегралы (5.12)—(5.14) можно значительно упростить, тем самым получить термодинамические характеристики электронов в металле. В дальнейшем для такого упрощения нам пригодится следующее качественное соображение. Согласно (5.15), при нулевой температуре плотность состояний постоянна и зависит лишь от химического потенциала при T=0, т. е. фактически лишь от числа электронов в системе. С другой стороны, из приведенных выше замечаний о вкладе в термодинамические свойства лишь электронов в узком «пояске» вблизи следует, что основной вклад в интегралы (5.12) — (5.14) будет давать область вблизи  .