Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 19

.                (4.57)

Значение радиуса aопределяется из условия

.                                          (4.58)

Удобные соотношения для термодинамических величин можно получить при низких и высоких по сравнению с температурой Дебая температурах, приближенно вычисляя интегралы (4.42, 4.43, 4.48, 4.50, 4.51) (Таблица 4.1). Видно, что при низких температурах теплоемкость кристалла изменяется пропорционально – иногда это называют законом «т-куба».

При высоких температурах теплоемкость стремиться к постоянному значению – соотношение Дюлонга - Пти, соответствующему идеальному газу системы из  таких частиц. Зависимость теплоемкости кристалла от температуры представлена на рис. 4.3.

Пропорциональность теплоемкости при низких температурах  выполняется и для оптических фононов.

4.5. Определение температуры плавления кристаллa

Полученные выше соотношения позволяют оценить еще одну важную характеристику твердого тела – температуру плавления . Хотя с ростом температуры число фононов возрастает, но пока температура тела мала , смещения атомов  от положения равновесия малы

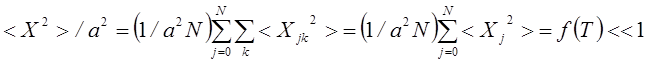.           (4.59)

Здесь а – равновесное расстояние между частицами кристалла, – средне квадратичное смещение частиц кристалла от положения равновесия в волне с волновым числом K

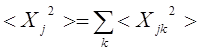.                                                                         (4.60)

Таблица 4.1

Таким образом, полученные выше соотношения, учитывающие вклад колебаний частиц, образующих кристалл, возле положения равновесия справедливы лишь при малых отклонениях <<1. Однако с ростом температуры, особенно при ее приближении к температуре плавления, интенсивность колебаний возрастает и вклад вносят уже нелинейные взаимодействия фононов. Будем считать, что температура плавления соответствует разрушению кристалла и это происходит, если средне квадратичное смещение частиц кристалла от положения равновесия становится порядка межчастичного расстояния

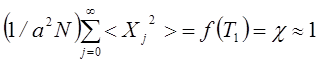.                                  (4.61)

Поменяв местами суммирование в формуле (1) 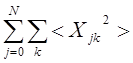 на 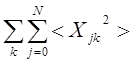 и учтя, что полная энергия в волне, состоящей из кинетической  и потенциальной   энергий равна , получим

.                                    (4.62)

Таким образом, средне квадратичное смещение частиц кристалла от положения равновесия может быть представлено в виде

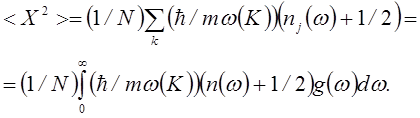                                  (4.63)

Используя функцию распределения Дебая

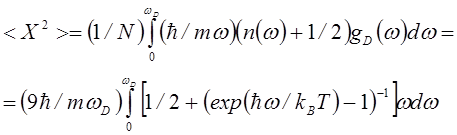
и проводя интегрирование при , получим

.                                        (4.64)

Подставив (4.64) в (4.63), получим оценку для температуры плавления кристалла

.                                    (4.65)

Поскольку , то температура плавления не зависит от массы частиц, образующих кристалл. Формула (4.65) носит название формулы Линдемана (G. Lindeman). Численные расчеты и сопоставления с экспериментом дают следующее значение для константы χ = 0.2.( Lindeman G.A.- Phys. Zs., 11, 609, 1910)..

В работе [Н.А.Сачавская. В.В.Евстигнеев, А.Ф.Сачавский, А.А.Сачавский. Единое уравнение для коэффициента вязкости. Труды АлтГТУ им. И.И.Ползунова, Барнаул, в.8, С. 197-206, см. http://elib.altstu.ru/elib/books/Files/pa2000_3/pages/08/pap_08.html] предлагается учет ангармонизма взаимодействия. 

В модели авторов, так же как и в теории Линдемана, плавление связывается с амплитудой колебания атомов около положения равновесия, но причиной разрушения решетки считаются силы ангармонического взаимодействия, т.е. при повышении температуры увеличивается не только амплитуда колебаний атомов, но и силы ангармонического взаимодействия.

Считается, что плавление начинается тогда, когда давление сил ангармонического взаимодействия G_a достигает значения величины модуля сдвига, соответствующего максимуму, т.е. температуре ноль градусов G_t0:

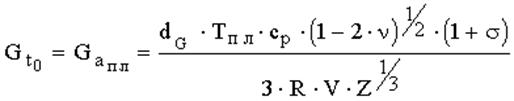 , (4)

где d_G- постоянная равная 3,2• 10⁵ Н• м• К^-1.