При рассмотрении поведения электронов
в кристалле обычно используют два важных предположения. Первое заключается в
пренебрежении влиянием движения атомов на энергетический спектр электронов.
Возможность такого подхода связана с существенным различием скоростей атомов и
электронов в твердом теле. Отношение скоростей атомов и электронов предстает в
виде ![]() , где c, М, ve, m — соответственно скорости и массы атомов и электронов.
При выполнении такого неравенства движение электронов определяется мгновенным
положением ионов (атомов), а медленное движение ионов происходит под действием
лишь среднего пространственного распределения электронов. Такое приближение
носит название адиабатического. Суть такого названия состоит в том, что
электроны адиабатически следуют за движением ионов, поэтому можно считать, что
электроны находятся просто в заданном потенциальном поле ионов. Если учитывать
влияние движения ионов на энергетический спектр электронов, то придем к
электрон-фотонному взаимодействию. В дальнейшем, однако, мы его не учитываем.
, где c, М, ve, m — соответственно скорости и массы атомов и электронов.
При выполнении такого неравенства движение электронов определяется мгновенным
положением ионов (атомов), а медленное движение ионов происходит под действием
лишь среднего пространственного распределения электронов. Такое приближение
носит название адиабатического. Суть такого названия состоит в том, что
электроны адиабатически следуют за движением ионов, поэтому можно считать, что
электроны находятся просто в заданном потенциальном поле ионов. Если учитывать
влияние движения ионов на энергетический спектр электронов, то придем к
электрон-фотонному взаимодействию. В дальнейшем, однако, мы его не учитываем.
Второе предположение при построении
энергетического спектра электронов в твердом теле состоит в пренебрежении
взаимодействием электронов друг с другом. Существуют способы, с помощью которых
многоэлектронную задачу удается свести к многоэлектронной (малоэлектронной?). Одним из таких
методов, например, является метод Хартри—Фока, основная идея которого
состоит в замене потенциальной энергии
электронов 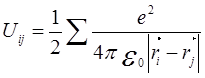 некоторым
эффективным потенциалом — внешним полем
некоторым
эффективным потенциалом — внешним полем ![]() , в котором каждый электрон движется независимо,
но в эффективном потенциальном поле, создаваемым всеми остальными зарядами.
Такое предположение позволяет описывать любой электрон индивидуальной волновой
функцией. Последнее обстоятельство существенно упрощает рассмотрение
энергетического спектра электронов в кристалле
, в котором каждый электрон движется независимо,
но в эффективном потенциальном поле, создаваемым всеми остальными зарядами.
Такое предположение позволяет описывать любой электрон индивидуальной волновой
функцией. Последнее обстоятельство существенно упрощает рассмотрение
энергетического спектра электронов в кристалле
5.3.1. Элементы теории возмущения
Рассмотренная выше теорема Блоха определяет вид волновых функций электронов в периодическом поле решетки. Дальнейшей задачей является определение энергетического спектра электронов в периодическом поле ионов, находящихся в узлах кристаллической решетки. Для этого необходимо воспользоваться уравнением Шредингера с периодическим потенциалом поля решетки. Эта задача, в общем случае, оказывается весьма сложной, и конечные результаты в данном случае в аналитическом виде удается получить лишь в двух предельных случаях: слабой связи, когда энергия взаимодействия электронов с решеткой мала по сравнению с кинетической энергией свободных электронов, и сильной связи, когда электроны почти локализованы в потенциальном поле атома и переходы от одного атома к другому совершаются за счет туннелирования. В обоих случаях нахождения энергетического спектра можно использовать стационарную теорию возмущения (см, например, [10]). Теории возмущения может быть использована, если Гамильтониан системы можно представить в виде суммы двух операторов
![]() ,
(5.40)
,
(5.40)
Здесь ![]() — оператор невозмущенной системы,
— оператор невозмущенной системы, ![]() - оператор возмущения (например, потенциальная
энергия взаимодействия электронов с ионами решетки, которая считается малой по
сравнению с энергией свободных электронов), δ << 1 – малый параметр
задачи.
- оператор возмущения (например, потенциальная
энергия взаимодействия электронов с ионами решетки, которая считается малой по
сравнению с энергией свободных электронов), δ << 1 – малый параметр
задачи.
При этом энергетический спектр {![]() } и волновые функции {
} и волновые функции {![]() } могут быть легко определены.
} могут быть легко определены.
![]()
![]() =
=![]()
![]() (5.41)
(5.41)
Волновую функцию общего Гамильтониана
электрона ![]() можно искать в
виде разложения по собственным функциям невозмущенного состояния, представив
ее в виде:
можно искать в
виде разложения по собственным функциям невозмущенного состояния, представив
ее в виде:
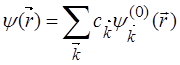 .
(5.42)
.
(5.42)
Подставляя (5.42) в уравнение Шредингера
![]()
![]() (5.43)
(5.43)
умножая его на ![]() , а затем интегрируя, с учетом
ортогональности собственных функций
, а затем интегрируя, с учетом
ортогональности собственных функций
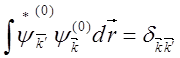 (5.44)
(5.44)
сведем задачу к системе
алгебраических уравнений для определения коэффициентов ![]() .
.
![]() .
(5.45)
.
(5.45)
Здесь ![]() - матрица с элементами
- матрица с элементами ![]() ,
, ![]() ,
, ![]() - вектор-столбец,
составленный из коэффициентов
- вектор-столбец,
составленный из коэффициентов ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.