Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 34

г) Полуметаллы

Выше рассматривался случай, когда при перекрытии зон в верхнюю переходит достаточно много электронов. Однако возможен случай, при котором в верхнюю зону переходит лишь незначительное количество электронов (см. рис. 5.13 г). Такие твердые тела называются полуметаллами. Типичными представителями этой группы тел являются As, Sb, Bi, у которых на атом приходится по пять электронов, но эти элементы кристаллизуются в решетку с двумя атомами на ячейку. В отсутствие перекрытия зон они представляли бы собой диэлектрики. Однако из-за слабого перекрытия валентной зоны и зоны проводимости возникает частично заполненная зона. На рис. 5.19 показана картина перекрытия зон в полуметаллах. Отметим, что концентрация электронов в зоне проводимости полуметаллов весьма мала: для Bi  т. е. на пять порядков ниже, чем у обычных металлов.

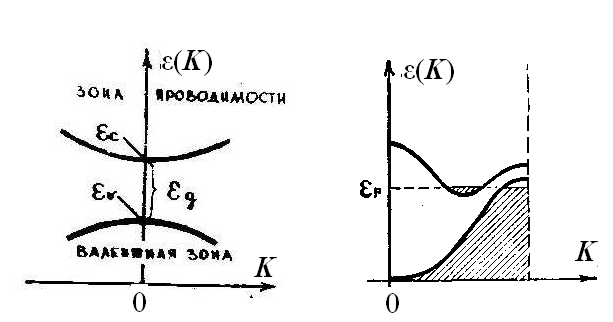
Рис.5.19                                              Рис. 5.20

5.5. Электроны и дырки в полупроводниках

Зная характер зонной картины полупроводников, можно рассмотреть статистику электронов в них. Ранее мы изучили статистику электронов в металлах, где было показано, что химический потенциал μ для металлов по порядку величины равен энергии Ферми  и медленно убывает с температурой. Такой результат был получен вследствие вырожденности электронов в металлах. В полупроводниках ситуация иная. Как было отмечено, полупроводники отличаются от диэлектриков лишь количественно величиной энергетической щели  между разрешенными полосами энергии (для типичного диэлектрика алмаза , а для типичных полупроводников: Si ; Ge ; Pb  ). Различают чистые (собственные) полупроводники и примесные (легированные). Очевидно, что в полупроводниках

                                      (5.114)

В обычных условиях (комнатные температуры) концентрация носителей тока в полупроводниках , в то время как в металлах . Схема энергетического спектра собственного полупроводника приведена на рис.5.20 (показаны лишь две зоны, — энергия потолка валентной зоны.  — энергия дна зоны проводимости,  — ширина щели между разрешенными полосами энергии).

Построим статистику и вычислим термодинамические величины собственного полупроводника. Рассмотрим структуру зонной схемы собственного полупроводника и определим концентрацию электронов в зоне проводимости в зависимости от температуры. Полное число электронов N₀ в полностью заполненной валентной зоне может быть записано (при T=0) в виде

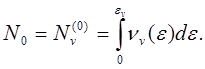                                       (5.115)

При температуре Т часть электронов находится в валентной зоне, и их концентрация в ней равна

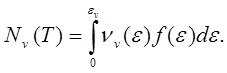                                                               (5.116)

Часть электронов при этом находится в зоне проводимости и их число определяется как

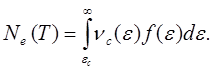                                 (5.117)

Ясно, что имеет место соотношение

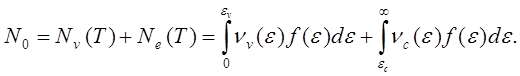                    (5.118)

где () и  < 0 — соответственно плотности электронных состоянии в валентной зоне и в зоне проводимости. Ясно, что   равно числу состояний, освободившихся в валентной зоне . При изучении полупроводников такие состояния обычно называют дырками; подробно этот вопрос будет изложен в кинетике. Следовательно, имеем

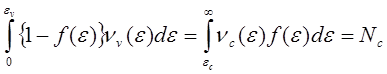                 (5.119)

Сделаем в (5.119) замены переменных в интеграле левой части , в интеграле правой  .  Тогда

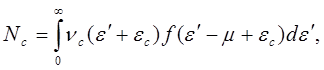                                (5.120)

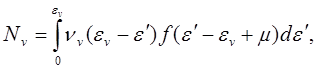                                (5.121)

где учтено, что

                        (5.122)

Предположим теперь, что уровень химического потенциала μ лежит в запрещенной зоне и выполняются соотношения:

(5.123)

Последнее означает, что уровень химического потенциала лежит значительно ниже дна зоны проводимости и значительно выше потолка валентной зоны. С учетом (5.123) функция распределения Ферми — Дирака превращается и распределение Больцмана

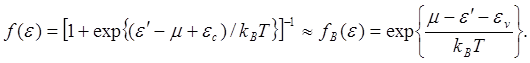                    (5.124)