Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 28

Важным результатом проведенного выше анализа является существование таких областей энергии, в которые электроны принципиально не могут попасть. Вид следа от поверхностей постоянной энергии на плоскости kx , ky показан на рис.5.6

Эти области обычно называют энергетическими щелями, иногда — запрещенными зонами. Разность соответствует максимальной величине энергетической щели. Таким образом, энергия электронов в кристалле так же, как, например, в атоме, является «дискретной» в том смысле, что существуют области запрещенных и разрешенных значений энергий. Подчеркнем, что в рассмотренном одномерном случае разрешенные и запрещенные зоны последовательно чередуются. В двух- и трехмерном случаях наблюдается, как говорят,  эффект перекрытия зон, который состоит в том, что минимум энергии в верхней зоне может находиться ниже максимума энергии в нижней зоне.

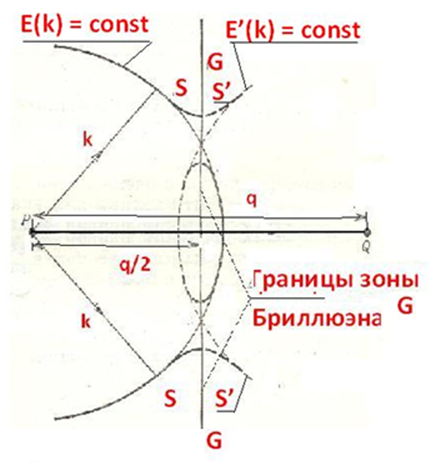
Рис.5.5

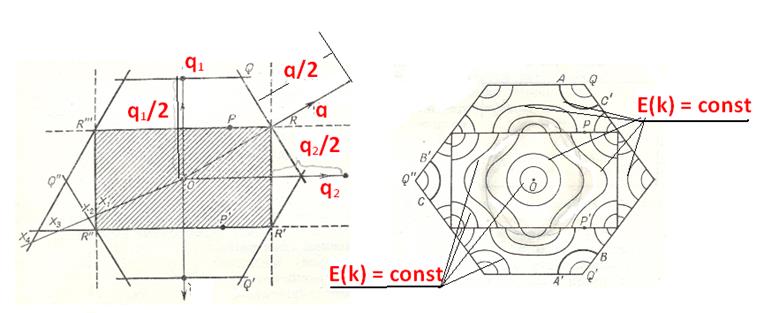
Рис.5.6

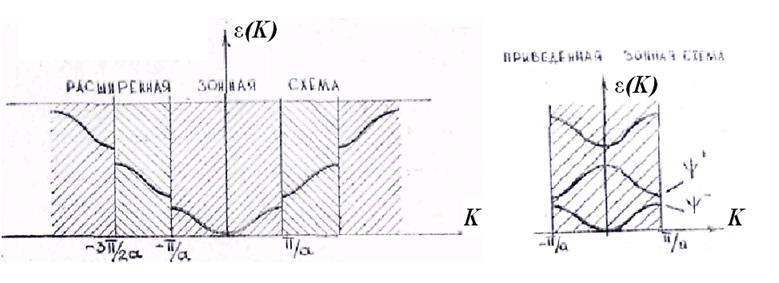
Рис.5.7                                                         Рис. 5.8

Заполнение электронами этих зон будет происходить, следовательно, в порядке возрастания энергии, а значит, при перекрытии зон может наблюдаться заполнение верхней зоны при незаполненной нижней [1, 2, 6]. Реально такой эффект наблюдается для целого ряда металлов. Зависимость для случая расширенных зон показана на рис. 5.7, а для случая приведенных зон — на рис. 5.8.

Теперь можно построить волновые функции, соответствующие ветвям  и . Согласно (5.65) для волновой функции с учетом взаимодействия имеем            

Из системы (5.66) с учетом значения корней уравнения (5.68), находим связь между константами

.                                                     (5.72)

Ограничиваясь одномерным случаем и положив 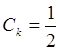 , получаем

;                                        

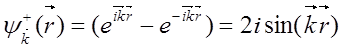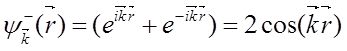.                                      (5.73)

Выражение (5.73) позволяет построить распределение плотности электронов для ветвей  и .

;

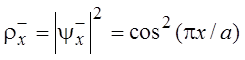.                         (5.74)

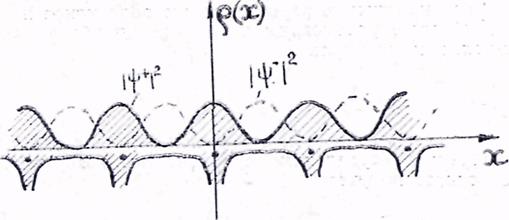
Рис. 5.9

Эти состояния представляют собой стоячую волну, состоящую из симметричных () и антисимметричных () волн, которая образовалась в результате отражения бегущей волны от решетки атомов (брэгговское отражение). На рис. 5.9 построено распределение плотности электронов в симметричной и антисимметричной волнах; здесь же показано изменение потенциала взаимодействия электронов с решеткой. Интересно, что электроны в состоянии с волновой функцией располагаются в основном между ионами решетки — эффект отталкивания, в состоянии с ; — сосредоточиваются вблизи ионов, поэтому испытывают в основном притяжение (энергия их ниже, чем у свободных электронов). В результате различия в энергиях состояний   и   возникает энергетическая щель.

Итак, воздействие потенциального периодического поля решетки на электроны приводит к тому, что энергия перестает зависеть от волнового вектора непрерывно, а испытывает скачки конечной величины на границе зоны Бриллюэна, когда волновой вектор кратен вектору решетки. Величина скачка при этом пропорциональна компоненте Фурье-преобразования потенциала решетки. Возникают энергетические зоны с величиной скачка в них  носящие название запрещенных. Между щелями возникают разрешенные зоны (см. выше о перекрытии зон): .

Заметим, наконец, что возможна еще одна трактовка воздействия потенциального периодического поля ионов на электроны. Для этого рассмотрим поведение  согласно уравнением (5.70) вблизи границ зоны Бриллюэна, когда волновые вектора  можно записать в виде

,       .                                       

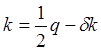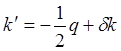При малых членом  под корнем в (5.70), можно пренебречь по сравнению с разностью невозмущенных уровней, откуда получаем

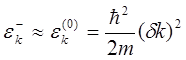                                          (5.75)

Таким образом, состоянию   при малых kсоответствует квадратичный закон дисперсии, как и в случае свободных электронов. Состоянию  при малых соответствует также квадратичный закон (для первой зоны )

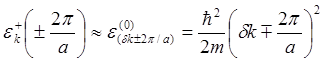.                                   (5.76)

На границах первой зоны Бриллюэна () (т. е. при брэгговском отражении), соответственно, имеем

,

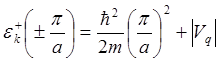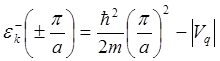,                  (5.77)