Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 9

а для показателя экспоненты должно выполняться условие

                                                           k p₁a₁ = 2πs₁,                                       (2.32)

где s₁ = 1, 2, 3…— произвольные целые числа. Установим область изменения целых чисел s₁. Из-за того, что вектор k изменяется в пределах зоны Бриллюэна - π/ a₁≤ k ≤ π/ a₁, из равенства (2.32) вытекает

-π/ a₁≤ k 2π s₁/p₁a₁≤ π/a₁

Следовательно, целые числа s₁ могут принимать следующие значения.

p₁/2≤ s₁ ≤ p₁/2.                                                             (2.33)

В трехмерном кристалле с цепочкой из p₁ ячеек размером a₁ в направлении оси , p₂ ячеек, размером a₂ в направлении оси и p₃ ячеек размером a₃ , в направлении оси, условия периодичности запишутся в виде

ψ_K(0) = ψ_K(0+a ), a = a.                                         (2.34)

В каждом из трех направлений целые числа s_j могут принимать следующие значения.

p_j/2≤ s_j ≤ p_j/2, j = 1,2,3.                                                (2.35)

Теперь можно подсчитать объем зоны Бриллюэна приходящейся на каждое состояние из этой зоны

Ω_B/p₁p₂p₃=  p₁p₂p₃= 8π³/ p₁a₁ p₂a₂ p₃a₃ = 8π³/V_c.          (2.36)

где V_c = p₁a₁p₂a₂p₃a₃ — объем кристалла.

Из (2.36) следует, что в кристалле больших размеров состояния в зоне Бриллюэнна распределены почти непрерывно.

3. КОЛЕБАНИЯ ЧАСТИЦ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ

Ранее кристалл рассматривался как геометрическое понятие, а атомы (ионы, молекулы) в узлах решетки покоились. Следующим естественным шагом в исследовании кристаллов является рассмотрение колебаний атомов в узлах решетки. С колебаниями кристаллической решетки в заметной мере связаны тепловые, оптические, кинетические и другие свойства твердых тел.

3.1. Колебания в одномерной цепочке (случай одного атома в ячейке)

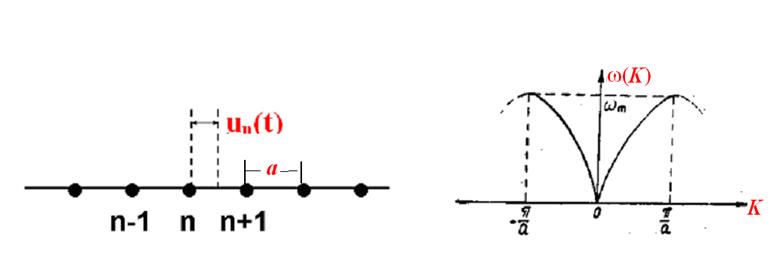
Простейшей моделью при изучении колебаний решетки является одномерная цепочка атомов (рис. 3.1). Сначала, рассмотрим эту задачу классически, полагая, что все частицы являются атомами одного сорта и в равновесии расположены на расстоянии а друг от друга. Это равновесное состояние атомов определяется условием минимума потенциальной энергии. Пусть и_п — смещение п-го атома из положения равновесия. С учетом смещения атомов полную энергию кристалла можно разложить в ряд Тейлора по смещениям, ограничиваясь лишь квадратичными членами. В этом случае полную энергию кристалла представим, как сумму статической энергии, которую имеет система в состоянии покоя U₀ , и энергии колебаний  = 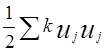, где k =:

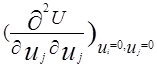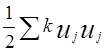 + .                                                 (3.1)

Классическое уравнение движения для п-гоатома есть

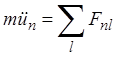,                                                                          (3.2)

где т — масса атома;  — вторая производная от смещения по времени; F_п1— сила, действующая на n-й атом со стороны l-го атома. Силы взаимодействия очень быстро убывают с расстоянием, поэтому (3.2) можно ограничиться только взаимодействием с ближайшими соседями. Согласно (3.1) при малых смещениях можно считать действующие между частицами силы пропорциональным смещениям:

                                          (3.3)

                          Рис. 3.1                                                                    Рис.3.2

С учетом (3.3) и, считая коэффициент жесткости одинаковым для всех атомов, k(n,l) = const, уравнение (3.2) примет вид

= -k (u_n— u_n+1) - k(u_n— u_n-1)                                       (3.4)

Таким образом, получили систему «зацепляющихся» уравнений. Несмотря на то, что в такой системе очень много уравнений (в принципе в бесконечной цепочке—бесконечно), можно определить характер колебаний цепочки благодаря следующей процедуре. Смещение любого атома п от положение равновесияu_n можно считать функцией от координаты r_п=па (п — целое число) u_n(па). Воспользовавшись результатом теоремы Блоха (1.28), будем искать решение (3.4) в виде плоской волны:

                                           и_п = и₀(t) ехр(iKпа).                 ·                               (3.5)