Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 15

где  (n—целое число) – вектор обратной решетки кристалла. Поэтому величина для фонона носит название квазиимпульса.

Вернемся теперь к вопросу о подсчете полной энергиии решетки, связанной с колебаниями частиц возле положения равновесия. Энергия кристалла согласно (3.29) может быть представлена в виде суммы по вкладам (в гармоническом приближении) от отдельных волн – вкладов от энергий отдельных фононов

                                                   (3.44)

Однако сами фононы описывают не все, а лишь возбужденное состояние кристалла. В энергию фононов не входят энергия нулевых колебаний атомов и энергия равновесного положения.

Обнаружить фононы в кристалле можно по взаимодействию фотонов с  кристаллом. Измеряя импульс и энергию подающей на кристалл электромагнитной волны заданной частоты (Рис.3.7), можно определить характеристики фонона q(рис.3.8), на котором произошло рассеяние

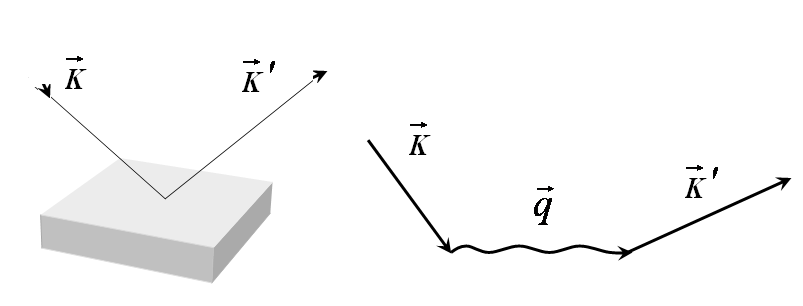
Рис.3.7.                                                              Рис.3.8

электромагнитной волны. Это можно сделать, используя, используя законы сохранения энергии  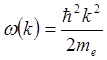и импульса

.

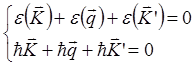Если в законах сохранения энергии и импульса произвести сокращение на общий множитель, то они примут вид

.

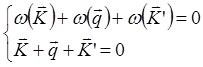Соотношения, аналогичные приведенным выше, возникают при анализе целого ряда коллективных возбуждений в жидкости и газе (например, в таких явлениях как турбулентность).

4. УРАВНЕНИЕ СОСТОЯНИЯ ТВЕРДОГО ТЕЛА

4.I. Свободная и внутренняя энергия кристалла

Используя полученные в предыдущем параграфе выражения для характеристик фононов (числа частиц в данном состоянии, свободной и внутренней энергий), определим теперь свободную и внутреннюю энергии фононной подсистемы, производя суммирование по всем волновым числам фононов:

                                                       (4.1)

Здесь суммирование производится по всей зоне Бриллюэна

Таким образом, вычисление термодинамических свойства кристаллической решетки сводится к решению задачи о статистике газа фононов, когда свободная энергия кристалла согласно может быть представлена в виде суммы по вкладам (в гармоническом приближении) от отдельных волн – вкладов от энергий отдельных фононов. Используя (3.39) для свободной энергии имеем

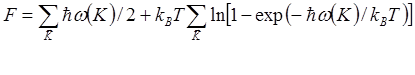,                                      (4.2)

При вычислении свободной энергии F возникает трудность, связанная с необходимостью знать спектр колебаний (спектр фононов) в кристалле (). Нахождение последнего сопряжено со значительными вычислительными трудностями. Существует, однако, метод, позволяющий несколько упростить расчет термодинамических функций. Он заключается в переходе от суммирования по всем нормальным колебаниям в формуле (4.2) к интегрированию по. В этом случае для свободной энергии приходим к формуле

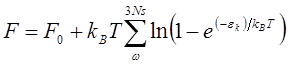.                    (4.3)

Используя (3.42) для внутренней энергии имеем

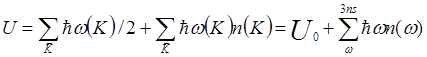.                     (4.4)

Здесь,  — свободная и внутренняя энергии, соответственно, атомов в положении равновесия (с учетом нулевых квантовых колебаний); величина , где— число атомов в кристалле;  — энергия одного атома в положении равновесия (фактически совпадающая с энергией связи), зависящая лишь от плотности тела, но не от температуры. Переход в (4.3), (4.4) к суммированию по всем  частотам. Такой подход правомерен, поскольку спектр  фактически является непрерывным. Теперь термодинамические функции решетки можно вычислить, если воспользоваться энергетическим спектром фононов в кристалле и с учетом распределения фононов по объему зоны Бриллюэна можно перейти в (4.3), (4.4) от суммирования к интегрированию по частотам, введя плотность состояния фононов — число фононов, приходящихся на интервал частот ω. Следовательно,  для произвольной функции () можно осуществить переход от суммирования к интегрированию, воспользовавшись следующим соотношением:

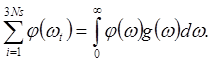                                            (4.5)

При использовании перехода (4.5) следует учесть, сто в сложных ячейках существует два типа колебаний: акустические и оптические — и, следовательно, два типа фононов: акустические и оптические.