Таким образом, колебания трехмерного кристалла со сложной
решеткой (в элементарной ячейке которой содержится s атомов) распадаются на три
акустические ветви и (3s—3) оптические ветви. На рис. 3.6 показаны
(схематически) зависимости ω(![]() ) для
разных ветвей спектра вдоль некоторого выбранного направления в кристалле
(совмещено несколько таких направлений, b—
вектор обратной решетки) при s = 3.
) для
разных ветвей спектра вдоль некоторого выбранного направления в кристалле
(совмещено несколько таких направлений, b—
вектор обратной решетки) при s = 3.
3.4. Фононы и их свойства. Энергия колебаний
Выше были рассмотрены простейшие виды
движения в кристаллах — колебания атомов (ионов, молекул) вблизи положения
равновесия. Такие движения естественно было изучать, используя собственные
колебания. Сама возможность рассмотрения собственных колебаний основана,
очевидно, на малости отношения смещения атомов из положения равновесия к
межатомному расстоянию ![]() << 1. Это позволило
рассмотреть различные колебания атомов в решетке как
систему независимых осцилляторов.
<< 1. Это позволило
рассмотреть различные колебания атомов в решетке как
систему независимых осцилляторов.
Хорошо известно, что
электромагнитные волны можно изучать с помощью введения понятия о частицах —
фотонах, имеющих определенную энергию ![]() и
импульс
и
импульс ![]() . Введение фотона удобно в целом ряде
случаев при исследовании взаимодействия электромагнитного поля с веществом. По
аналогии с фотоном в конденсированных телах также можно ввести элементарные
возбуждения (квазичастицы), удобные для описания свойств твердых тел.
Фактически вся современная теория конденсированных тел базируется на понятии
квазичастицы.
. Введение фотона удобно в целом ряде
случаев при исследовании взаимодействия электромагнитного поля с веществом. По
аналогии с фотоном в конденсированных телах также можно ввести элементарные
возбуждения (квазичастицы), удобные для описания свойств твердых тел.
Фактически вся современная теория конденсированных тел базируется на понятии
квазичастицы.
Поясним термин «квазичастица»
на примере колебаний атомов в кристалле. Поскольку отдельные атомы взаимодействуют
между собой, то не существует их независимого движения. Простейшим типом
движения в кристалле, следовательно, является не движение отдельного атома, а
смещение группы атомов. Хотя ранее и было показано, что такое смещение
отличается в кристаллах с простой и сложной ячейками, но в данном случае тип
ячейки не существен. Важно, что имеет место коллективный эффект — волна
смещения атомов. Распространение такой волны в кристалле приводит к
периодической зависимости ![]() от
от ![]() . Если рассматривать квантовую
теорию колебаний кристаллической решетки, то можно доказать, что существуют
элементарные возбуждения в кристалле, похожие на частицы и обладающие
наименьшей порцией энергии при заданной частоте. Для колебаний кристаллической
решетки такие квазичастицы называются фононами. Здесь термин
«квазичастица» употребляется потому, что такое элементарное возбуждение не
может существовать вне кристалла как свободная частица (как, например, фотон).
С квантованием колебаний кристаллов, при котором естественным образом
появляются квазичастицы, можно познакомиться в [7,11]. Отметим, что фононы,
как и другие квазичастицы, — вполне реальные объекты в конденсированной среде:
их можно обнаружить, например, при рассеянии реальных частиц, падающих на
конденсированное тело.
. Если рассматривать квантовую
теорию колебаний кристаллической решетки, то можно доказать, что существуют
элементарные возбуждения в кристалле, похожие на частицы и обладающие
наименьшей порцией энергии при заданной частоте. Для колебаний кристаллической
решетки такие квазичастицы называются фононами. Здесь термин
«квазичастица» употребляется потому, что такое элементарное возбуждение не
может существовать вне кристалла как свободная частица (как, например, фотон).
С квантованием колебаний кристаллов, при котором естественным образом
появляются квазичастицы, можно познакомиться в [7,11]. Отметим, что фононы,
как и другие квазичастицы, — вполне реальные объекты в конденсированной среде:
их можно обнаружить, например, при рассеянии реальных частиц, падающих на
конденсированное тело.
К понятию фонона можно
подойти и другим образом. Если бы мы захотели подсчитать энергию решетки
заключенную в колебаниях N
частиц возле своего узла
![]() кол то исходя их (3.1) должны были бы записать
кол то исходя их (3.1) должны были бы записать
![]() кол =
кол = 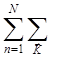
![]() (3.28)
(3.28)
Здесь производится суммирование по всем атомам
решетки ![]() и
и![]() по всем волновым векторам
по всем волновым векторам ![]() из зоны
Бриллюэна для каждого атома, так как. каждая волна дает свой вклад в смещение.
В сумме (3.29) можно поменять местами порядок суммирования, записав это
выражение так
из зоны
Бриллюэна для каждого атома, так как. каждая волна дает свой вклад в смещение.
В сумме (3.29) можно поменять местами порядок суммирования, записав это
выражение так
![]() кол = =
кол = = 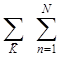
![]()
![]() =
=
![]() ε(
ε(![]() ). (3.29)
). (3.29)
Здесь ε(![]() )
— энергия волны с волновым вектором
)
— энергия волны с волновым вектором ![]() с учетом вклада от всех
N атомов решетки. Выражение
(3.29) можно использовать и в квантовом случае, но подсчитав энергию каждой
волны в рамках квантовой механики.
с учетом вклада от всех
N атомов решетки. Выражение
(3.29) можно использовать и в квантовом случае, но подсчитав энергию каждой
волны в рамках квантовой механики.
Прежде напомним некоторые сведения из
статистической физики, относящиеся к квантовым частицам. Для частиц с целым
спином подчиняющимся статистики Бозе-Эйнштейна (S.N. Bose, A. Einstein), термодинамический потенциал квантового состояния ![]() связан с числом заполнения
связан с числом заполнения ![]() соотношением [11] .
соотношением [11] .
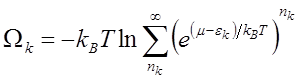 (3.30)
(3.30)
Суммирование геометрической прогрессии в (3.30) дает выражение
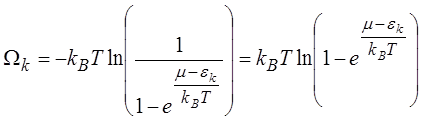 (3.31)
(3.31)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.