Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 35

Аналогично ведет себя функция распределение дырок по энергиям . Подставляя (5.124) в (5.120) получаем зависимость концентрации электронов проводимости от температуры

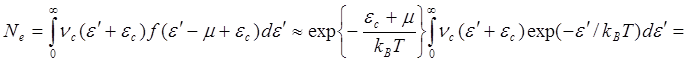
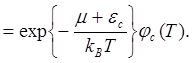                                      (5.125)

Аналогично находим зависимость концентрации от температуры для дырок в валентной зоне

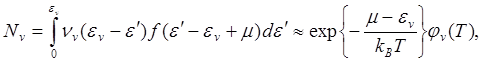            (5.126)

где и  равны

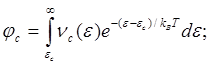                                    (5.127)

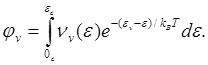                                      (5.128)

Поскольку уровень химического потенциала еще не определен, ничего нельзя сказать о концентрации электронов в валентной зоне и зоне проводимости при температуре Т. Однако произведение не зависит от химического потенциала µ:

             (5.129)

Выражение (5.129) можно упростить, если вспомнить, что в собственном полупроводнике . Тогда из (5.129) получаем

                              (5.130)

Сравнивая формулы (5.125) и (5.126) с (5.130),

=

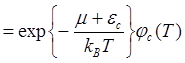получаем

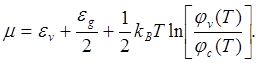                                (5.131)

Вычислим в явном виде полученные функции , , задав вид плотности электронных состояний  и . В полупроводниках закон дисперсии имеет квадратичный вид [6]:

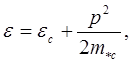
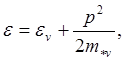                                        (5.132)

где   — эффективные массы соответственно электронов в зоне проводимости и в валентнойзоне (вблизи экстремумов энергии); — экстремумы соответствующих энергетических зон (— максимум валентной зоны:  — минимум зоны проводимости, см. рис. 5.16). С учетом соотношении (5.132), для плотностей состояния электронов и дырок имеем

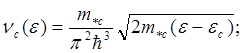                               (5.133)

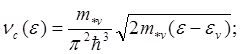                                (5.134)

Тогда функции и  можно вычислить и определить их зависимость от температуры:

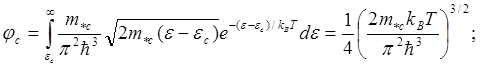    (5.135)

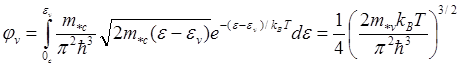.     (5.136)

Из формулы (5.136) получаем зависимость электронов проводимости и дырок от температуры для собственного полупроводника

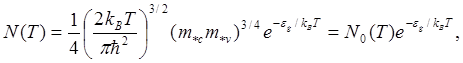    (5.137)

Наконец находим химический потенциал

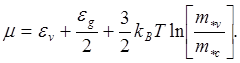                                     (5.138)

Из соотношения (5.138) видно, что при T= 0, если положить , получаем 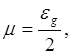т. е. химический потенциал расположен точно посередине запрещенной зоны. Кроме того, поскольку , то  не может отстоять от середины уровня запрещенной зоны более чем .

Теперь нетрудно оценить внутреннюю энергию и теплоемкость полупроводника, с учетом вклада электронов в зоне проводимости и дырок в валентной зоне. Вычисляя внутреннюю энергию полупроводника аналогично случаю электронов в металле функцию  с учетом невырожденности электронов в полупроводниках () получаем

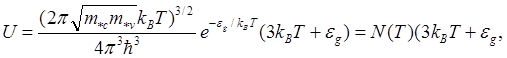              (5.139)

где N(T) определяется из (5.137).

Для теплоемкости имеем

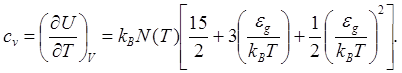                    (5.140)

Функция имеет максимум при  откуда

                                                    (5.141)

Нетрудно оценить отношение электронной теплоёмкости в собственном полупроводнике к теплоемкости решетки. Вспоминая, что при рассматриваемых температурах  ( — концентрация атомов в 1 см³), имеем

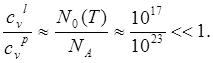                               (5.142)

Таким образом, электронная теплоемкость в полупроводнике всегда много меньше решеточной.

Оглавление

Предисловие                                                                                                                      2

Введение                                                                                                                             2

1. СВОЙСТВА КРИСТАЛЛИЧЕСКИХ ТВЁРДЫХ ТЕЛ                                            12

1.1 Простейшие свойства кристаллических структур                                                  12

1.1.1. Типы связей                                                                                                                12

1.1.2. Симметрия                                                                                                                 16

I.2. КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА ТВЕРДОГО ТЕЛА                                     17

1.2.1. Геометрическая структура кристаллов. Решетка Бравэ                                       17