Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 2

Вспоминая уравнение состояния в вириальной форме для неидеальных газов, которое учитывает парные и тройные взаимодействия. Однако, такое разложение не приемлемо для жидкости. Почему, не смотря на близкое значение параметра взаимодействия, твёрдые тела и жидкости ведут себя по-разному? Рассмотрим объёмы порядка радиуса взаимодействия для твёрдого тела и жидкости (рис.4). Посмотрим на твёрдое тело в момент времени  . Условно будем рассматривать четыре частицы и, обратим внимание, что все они находятся на одинаковых расстояниях от той частицы, которую рассматриваем. В жидкости картина иная: тут тоже рассматривается четыре частицы, но все они находятся на разных расстояниях. Очевидно, что параметр взаимодействия и в том и в другом случае одинаков, но конфигурация разная!

Возьмём другой момент времени (рис.4). Т.к. условия взаимодействия остались прежними, то радиус взаимодействия не изменился. В твёрдом теле ничего не изменилось, а в жидкости всё может оказаться по-другому. Число частиц осталось прежним, но в результате изменения конфигурации в жидкости суммарная энергия изменила своё значение. В твёрдом теле суммарная энергия осталось прежней.

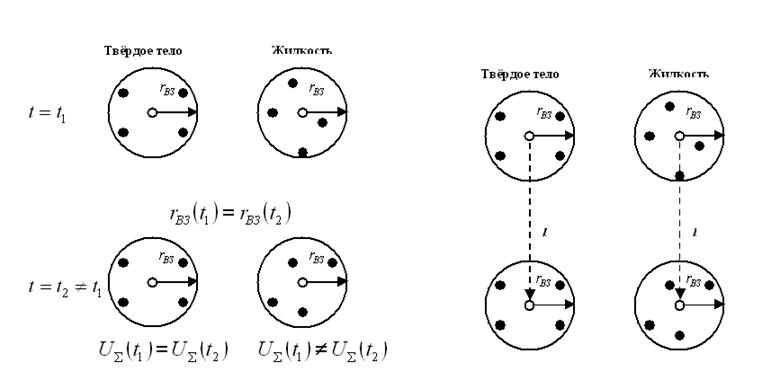
Рис. 4                                                          Рис. 5

Более того, если рассмотреть сдвиг частиц не по времени, а в пространстве

(рис.5) на расстояние l , то окажется, что для твёрдого тела есть такое расстояние, при перемещении на которое твёрдое тело сохраняет своё строение. Если соблюдается это свойство, то говорят, что в твердом теле существует дальний порядок. В жидкости дальний порядок не сохраняется, а сохраняется ближний порядок, если под ним понимается число частиц в сфере взаимодействия. 

В рамках какого анализа необходимо рассматривать взаимодействие частиц: классического или квантового? Для ответа на этот вопрос надо ввести критерий вырождения, представляющий собой отношение двух характерных величин

 

1 Квантовый подход

                            

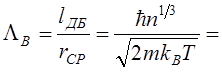
где 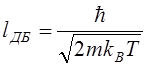  – длина волны Де Бройля.

Таким образом, если длина волны Де Бройля существенно меньше, чем характерное расстояние между частицами, то можно пользоваться классической механикой, а если больше или порядка единицы, то квантовой.

Глядя на критерий вырождения ясно, что при стремлении температуры к нулю, эта величина всегда будет сколь угодно больше единицы, т.е. для того чтобы объяснить, что там происходит, нужен квантовый подход.

Без квантовой механики нельзя объяснить ряд экспериментальных зависимостей в физике твёрдого тела (рис. 6 – 8).

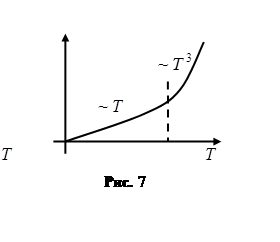
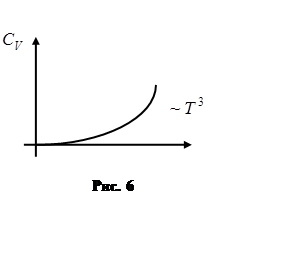
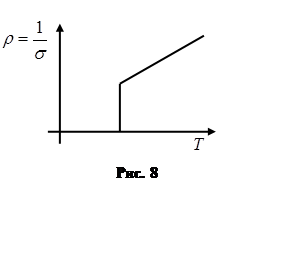
На рис. 6 и 7 показаны результаты чисто теплофизических экспериментов –зависимости теплоёмкости материала от температуры. На рис. 6 характерном для диэлектриков при стремлении температуры к нулю теплоёмкость обращается в ноль, а при возрастании температуры – теплоёмкость возрастает пропорционально температуре в третьей степени. Другой пример показан на рис.7, где изображена зависимость от температуры теплоёмкости металлов вблизи нуля. Следующий пример (рис. 8) демонстрирует обращение изменения сопротивления некоторых металлов и обращения его в ноль при температурах ниже критических. Это явление называется сверхпроводимостью материалов. Такие зависимости не только качественно, но и количественно находят свое объяснение только в рамках квантовой механики и демонстрируют то, что без применения квантовых подходов нельзя существенно продвинуться в изучении теории конденсированного состояния вещества.

Вернёмся к рассмотрению выражения для параметра вырождения 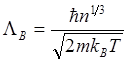. Видно, что может существовать область конденсированного состояния вещества, где оно находится в жидком состоянии, но тем не менее является квантовым, т.к. длина волны Де Бройля помимо температуры зависит ещё и от массы, которая увеличивается с возрастанием атомного номера вещества. Для самых лёгких веществ, таких как водород и гелий, можно получить, что они будут находиться в жидком, но быть и в квантовом состоянии (квантовые жидкости). Чтобы получить водород в твёрдом состоянии т.е. достичь условий, когда параметр взаимодействия окажется больше единицы, нужно существенно увеличивать концентрацию, т.е. повышать давление.