ВВЕДЕНИЕ
В учебном пособии «Термодинамические и статистические свойства твердых тел» [17] были изучены свойства решетки твердого тела и электронов в состоянии термодинамического равновесия. Теперь обратимся к исследованию процессов, протекающих в неравновесных условиях. Этот круг вопросов относится к физической кинетике твердого тел.а.
1. ФИЗИЧЕСКАЯ КИНЕТИКА ЯВЛЕНИЯ В ТВЕРДОМ ТЕЛЕ
В настоящей главе изложены вопросы, связанные с изучением кинетики элементарных возбуждений (квазичастиц) в твердых телах на основе кинетического уравнения Больцмана.
1.1. Кинетическое уравнение Больцмана
Многие физические явления, протекающие в твердых телах, удается успешно
описать на основе понятия элементарных (возбуждений (квазичастиц) и взаимодействия
между ними
(напомним, что электроны, фононы и т. д. в твердом теле отличаются от обычных
частиц в .вакууме наличием квазиимпульса, определенного лишь с точностью до
периода обратной решетки). В твердом теле квазичастицы могут рассматриваться как свободные,
взаимодействующие только за счет столкновений. При этом систему квазичастиц (электроны, фононы, и т. д.) можно
рассматривать как разреженный газ. Описание процессов в разреженном газе
квазичастиц, так же, как и в обычном разреженном газе, производится с помощью функции распределения
![]() , причем произведиие
, причем произведиие ![]() d3rd3vсоответствует числу
квазичастиц, находящихся в данный момент времени tв области d3rd3vфазового пространства.
Интегрирование по объёму твёрдого тела V и по всем возможным
скоростям даёт полное число квазичастиц
d3rd3vсоответствует числу
квазичастиц, находящихся в данный момент времени tв области d3rd3vфазового пространства.
Интегрирование по объёму твёрдого тела V и по всем возможным
скоростям даёт полное число квазичастиц
![]() d3rd3v=N (1.1)
d3rd3v=N (1.1)
Вместо функции
распределения ![]() при описании кинетики в твердом теле удобно
использовать функцию
при описании кинетики в твердом теле удобно
использовать функцию ![]() , где
, где![]() — квазиимпульс или функцию
— квазиимпульс или функцию ![]() , где
, где ![]() =
=![]() /
/![]() — волновой вектор квазичастиц.
— волновой вектор квазичастиц.
В
кинетике разреженного газа функция ![]() подчиняется уравнению
Больцмаиа [1, 2]
подчиняется уравнению
Больцмаиа [1, 2]
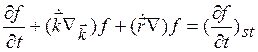 (1.2)
(1.2)
Здесь
![]() =d
=d![]() /dt,
/dt, ![]() = d
= d![]() /dt,
/dt, ![]() ,
, 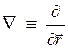 .
.
Отметим, что запись (1.2) означает возможность описания квазичастиц одновременно заданием
координат и импульсов ![]() и
и ![]() . Естественно, что это
возможно лишь при выполнении определенных критериев. Последние заключаются в следующем. Если
неопределенность координаты есть Δr (по порядку величины
благодаря соотношению неопределенностей она равна 1/Δk), то она должна быть
значительно меньше длины свободного пробега квазичастиц. С другой стороны, поскольку Δk
. Естественно, что это
возможно лишь при выполнении определенных критериев. Последние заключаются в следующем. Если
неопределенность координаты есть Δr (по порядку величины
благодаря соотношению неопределенностей она равна 1/Δk), то она должна быть
значительно меньше длины свободного пробега квазичастиц. С другой стороны, поскольку Δk![]() k, то
k, то
1/k = λв<<l(1.3)(1.3)
где λв — дебройлевcкая длина волны
квазичастиц. Ниже мы увидим, что l~![]() , где τ — время
релаксации; m* — эффективная масса квазичастицы. Следовательно, λв <<
, где τ — время
релаксации; m* — эффективная масса квазичастицы. Следовательно, λв << ![]()
1.2. Интеграл столкновений
Обратимся к
исследованию правой части уравнения Больцмана (1.2), носящей название интеграла
столкновений. Если бы квазичастицы не взаимодействовали друг с трутом (и с квазичастицами другого
сорта), то интеграл столкновений обратился бы в нуль. Действительно, в
этом случае df/dt, равная левой части уравнения (1.2), обращается
в нуль, поскольку
(вдоль траектории фазового пространства (![]() ,
, ![]() ) функция распределения не меняется.
) функция распределения не меняется.
Пусть W(k', k)dk' есть вероятность того, что за единицу времени квазичастица с волновым вектором ![]() в результате столкновения попадает в часть фазового объема
в результате столкновения попадает в часть фазового объема ![]() вблизи волнового
вектора
вблизи волнового
вектора ![]() . Величина
W(k, k')dk, в свою очередь, есть вероятность в
единицу времени перехода из состояния в состояние
. Величина
W(k, k')dk, в свою очередь, есть вероятность в
единицу времени перехода из состояния в состояние ![]() из части фазового объема
из части фазового объема ![]() . Нетрудно понять, что число переходов из состояния
. Нетрудно понять, что число переходов из состояния ![]() пропорционально числ квазичастиц в элементе фазового объема, т. е. функции распределения f(
пропорционально числ квазичастиц в элементе фазового объема, т. е. функции распределения f(![]() ). Соответственно число переходов из
). Соответственно число переходов из ![]() пропорционально f(
пропорционально f(![]() ). Таким образом, интеграл столкновений, характеризующий переходы между
состояниями
). Таким образом, интеграл столкновений, характеризующий переходы между
состояниями ![]() и
и
![]() за счет взаимодействия (которые
характеризуются величинами W(
за счет взаимодействия (которые
характеризуются величинами W(![]() ,
,![]() ) и W(
) и W(![]() ,
,![]() ), могут быть записаны в виде
), могут быть записаны в виде
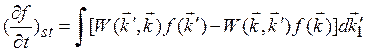 (1.4)
(1.4)
Если рассматривать парные столкновения квазичастиц, когда состояния и той, и другой частиц меняется, то интеграл столкновений, как нетрудно показать, примет вид (![]() ,
,![]()
![]() ,
,![]() ):
):
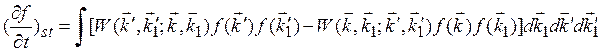 (1.5)
(1.5)
Последнее выражение
соответствует известному из кинетической теории газов выражению для 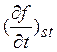 .
.
Бели в (1.5)
подставить равновесные функции f0, то интеграл
столкновений 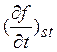 t, по определению,
обратится в нуль и отсюда
следует, что
t, по определению,
обратится в нуль и отсюда
следует, что
![]() =
=![]() (1.7)
(1.7)
Если при
столкновениях сохраняется (это имеет место т. е. Е+Е1 = ![]() , то получаем принцип детального равновесия:
, то получаем принцип детального равновесия:
![]() =
=![]() (1.8)
(1.8)
Принцип детального
равновесия (1.8) устанавливает равенство вероятностей прямых и обратных процессов.
Нетрудно видеть, что и для случая (1.4) он имеет место, т. е. ![]() =
= ![]() . Используя этот принцип, соотношения (1.4) и (1.5) можно записать:
. Используя этот принцип, соотношения (1.4) и (1.5) можно записать:
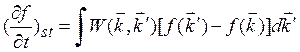 (1.4)
(1.4)
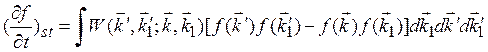 (1.5)
(1.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.