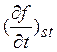Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 6

                                              = I_pp(f_p) + I_pd(f_p) + I_pg(f_p) + I_pe(f_p)                           (2.2)

десь I_pp, I_pd, I_pg, I_pg— соответственно интегралы столкновений фононов между собой, с электронами, дефектами и границей тела, а при изучении колебаний решетки мы ограничивались гармоническим приближением, т.е, в разложении потенциальной энергии решетки в ряд по степеням отклонений да положений равновесия ограничивались квадратичными членами. В таком приближении получились невзаимодействующие нормальные колебания, которые на квантовом языке отвечают фононам. Учет ангармонических членов в разложении потенциальной энергии, как уже отмечалось, приводит к взаимодействию фононов. Рассмотрим качественный вид интеграла столкновений /_РЛЫ- Фонолы подчиняются статистике Возе — Эйнштейна и в равновесии их функция распределения является планковской: f^ν_p0() = [ехр(ε^ν//k_BT) — 1]^-1, где ε^v= (в предыдущей части пособия функция f_p0() обозначена n_k). В неравновесном состоянии такое распределение нарушается. Поясним это на примере взаимодействующих друг с другом фононов. При учете ангармонизма решётки ки отдельные состояния фононов уже не являются стационарными: между ними могут происходить квантовые переходы. В результате любого перехода могут изменяться числа заполнения данного состояния, описываемые функцией распределения  f_p0(). Если, однако, энгармонизм мал, то переводы происходят редко по сравнению с частотами колебаний решетки (или с периодом колебаний). Следовательно, в промежутках между переходами фононы можно рассматривать мак свободные. Таким образом, условием применимости уравнения (2.1) является ω_pτ_p>>1 {τ_p— характерное время между столкновениями фононов). Квантовые переходы соответствуют как раз фонон-фононным взаимодействиям. Дай качественное объяснение причине нарушения равновесного распределения фононов в результате их взаимодействия между собой, сделаем одно важное замечание. Согласно распределению Планка, число фононов зависят от температуры тела, поэтому оно, вообще говоря, не сохраняется. Teм самым кинетика газа фононов отличается от .кинетики обычного газа: имеющие место в последнем парные столкновения, если они упругие, всегда приводят в конечном (после рассеяния) состоянии к тому же числу частиц, что я в начальном. Для фононов это совсем не так: sконечном состоянии могут наблюдаться и два, и три фонона в зависимости от дополнительных условий. К сожалению, мы не имеем здесь возможности изложить довольно громоздкий способ получения соответствующего интеграла столкновений [2, 7]. Следует, однако, проанализировать одно получающееся при этом следствие. Оно связано с тем обстоятельством, что при исследовании процессов рассеяния фононов друг на друге возможны две противоположные ситуации, обязанные своим существованием периодичности решетки.

Пусть, например, изучается процесс слияния двух фононов в один +=или распад фонона на два =+(этому .процессу соответствует учет кубических членов в разложении потенциальной энергии кристалла). При этом интеграл столкновений отличен от нуля, если только A-++=,где —вектор обратной решетки (вывод этого соотношения можно найти, например, в [5, 7, 8]). Это условие, в свою очередь, сводится к двум равенствам:

++=0                                        (2.3)

++=                                       (2.4)

где  —вектор, составленный из трех основных векторов обратной решетки в -пространстве. Условия (2.3) или (2.4) оказываются существенными для всей кинетики фононов. Первое из них — (2.3) — означает, что в трехфононных процессах суммарный импульс фононов сохраняется. Процессы, идущие с сохранением суммарного импульса, называют нормальными (или -процессами). Условие (2.4) означает, что в трехфононных процессах полный импульс не сохраняется. Проиллюстрируем этот вид взаимодействия, фононов на рис. 2.1. Из этого рисунка видно, что возможна ситуация, когда

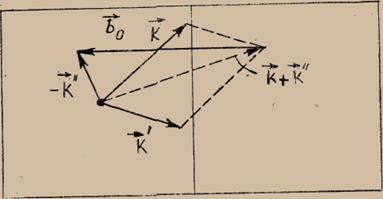
Рис. 2.1