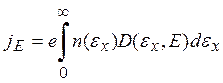Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 32

                                                                                                     (5.22)

где  — число электронов, падающих на единицу площади поверхности тела;  — коэффициент прозрачности потенциального барьера на поверхности металла, который определяется отношением интенсивностей (квадратов амплитуд) -прошедшей через барьер и падающей на барьер электронной волны, т. е. D(ε_x, E) = |C₁|²/|C₀|², где С₀—амплитуда падающей волны ψ₀(х) = С₀ехр (ik_xx). Исходя из этого и воспользовавшись (5.21), можно получить

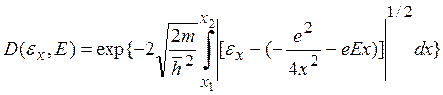                             (5.23)

Выражение (5.22), воспользовавшись распределением Ферми—Дирака, можно написать в виде

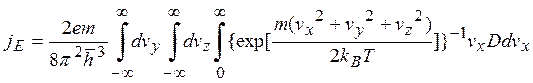                                 (5.24)

В результате подстановки (5.23) в (5.24) и последующего интегрирования получается (опущены несущественные члены)

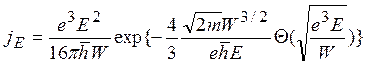(5.25)

где 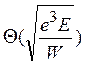—так называемая функция Нордгейма, которая физически выражает отношение уменьшения работы выхода за счет эффекта Шоттки к истинной работе выхода. Эта функция в настоящее время затабулирована для широкого диапазона входящих в нее параметров [16].

Согласно, (5,25), для плотности тока можно записать выражение

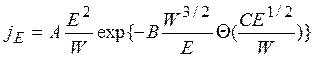                                                     .         (5.26)

где А=1,55-10^-6; В=6,85-10⁷; С=3,62-10^-4.Оценки плотности автоэлектронной эмиссии при         Е=6-10⁷ В/см (W=4,5эВ) дают ~10⁷ А/см², что близко к экспериментально измеренной величине. Отметим, что формулу (5.26) часто называют формулой Фаулера—Нордгейма. Нетрудно заметить, что она формально схожа с формулой Ричардсона—Дзшмана для термоэмиссии, если заменить в последней температуру на величину поля (с точностью до коэффициентов).

5.4. Автотермоэлектронная эмиссия

Теперь обратимся к случаю, когда температура тела отлична от нуля II действует достаточно сильное электрическое поле. В случае Т>0 часть электронов находится выше уровня Ферми ε_F и тем самым для них облегчен переход через потенциальный барьер. Не останавливаясь на вычислениях (см., например, [8, 16]), запишем сразу явное выражение для плотности автотермоэлектронного тока

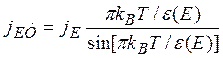                                                                                                                 (5.27)

где 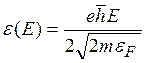— энергия, набираемая электронами в поле Е на длине волны де Бройля 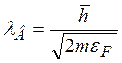;  — плотность автоэлектронного тока. Соотношение (5.27) справедливо, если >(ε > ε^*(T)) Возникновение отношения ε/k_BTфизически связано с учетом вклада различных энергетических зон электронов.

Представляет интерес рассчитать поток энергии, переносимый электронами в процессе эмиссии (в частности, этот вопрос важен при разработке термоэмиссионных преобразователей)

Вполне понятно, что уходящие с поверхности в результате эмиссии электроны могут уносить с собой энергию, что приводит к охлаждению тела. Эффект изменения температуры металла в процессе термоавтоэлектронной эмиссии носит название эффекта Ноттингама [161, Понятно, что проявление этого эффекта заметно лишь в случае, когда энергия, уносимая электронами при эмиссии, соизмерима с энергией, запасенной в теле, т. е. при больших плотностях тока. Подобное явление связано с отличием средней энергии ε_e, электронов, уходящих с поверхности, от средней энергии ε_e0электронов вдали от поверхности внутри кристалла. Разность этих энергий компенсируется обменом энергией между электронами и решеткой, приводя к охлаждению или нагреву тела. Кроме этого, протекание тока высокой плотности само приводит к тепловыделению (эффект Джоуля).

Вычислим поток тепла для термоэлектронной эмиссии, согласно соотношению

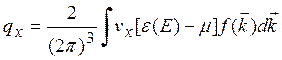                                                                             (5.28)

Подставляя в (5.28) значения к(Е) и f(k), получим

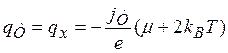                                                                                                                       (5.29)

Следовательно, поток тепла, уносимый электронами, складывается из потенциальной энергии, равной работе выхода μ и кинетической энергии теплового движения ~k_BT. Отметим, что, например, в термоэмиссионных преобразователях при j=20 А/см², T~2-10³К тепловой поток составляет величину q_т~70 Вт/см², в то время как излучение поверхности тела, нагретого до такой температуры, q_т~20 Вт/см².