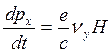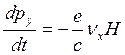Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 24

,                                           (3.132)

можно сделать вывод, что траектории в импульсном и координатном пространствах отличаются лишь масштабом и повернуты друг относительно друга на 90°.Нетрудно получить из (3.132)

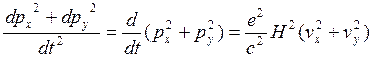         (3.133)

Но — элемент длины траектории электрона в импульсном пространстве. Тогда из (3.133) получаем

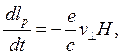
         (3.134)

откуда

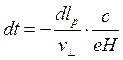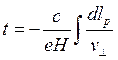,          (3.135)

Из соотношения (3.134) в случае замкнутости траектории электрона в магнитном поле можно получить период его движения (интегрирование производится вдоль замкнутой траектории в -пространстве):

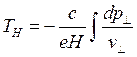        (3.136)

Введем   площадь   поверхности,   ограниченную   кривой   , согласно выражению

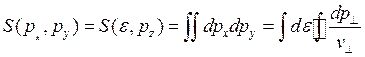          (3.137)

Теперь можно записать

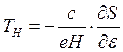           (3.138)

Здесь использовано, что . Величину т_н= dS/d называют эффективной циклотронной массой. Она является, естественно, функцией ε и , т. е. т_н= т_н (ε, ). Теперь нетрудно получить выражение для периода и частоты обращения электрона (циклотронной или ларморовской частоты:

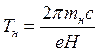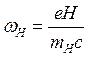,         (3.139)

Поскольку т_н= т_н (ε, ), то T_H=T_H(ε, ), ω_H=ω_H(ε, ), т. е. разные электроны вращаются со своими циклотронными частотами, зависящими от ε и ,. Заметим, что свободные электроны в магнитном поле (например, в обычной газовой плазме) все вращаются с одной и той же частотой _н=еН/тc. Кроме этого, поскольку наряду с электронами, движущимися по замкнутым орбитам, есть и электроны с открытыми траекториями, последние вообще не совершают ограниченного движения (эта ситуация невозможна в газе свободных электронов). С учетом указанных обстоятельств динамика квазиэлектронов в магнитном поле имеет важные существенные особенности [14].

Посмотрим теперь, как движется электрон, например, вблизи минимума е, т. е. беря простейший закон дисперсии =₀+р²/2m_*, получим

Отсюда имеем S=π|р|²=2πm_*,(-₀)-πр_г². Тогда получаем для эффективной массы                   т_н= dS/d = т*. Следовательно, вблизи дна зоны проводимости циклотронная масса совпадает с эффективной, причем т*>0 (носители являются электронами). Последняя ситуация наблюдается, когда в зоне мало электронов и все они сосредоточены вблизи ее дна.

Пусть теперь ε находится в области максимума. Тогда =₀ - р²/2m_*, откуда получаем S=π|р|²=2πm_*,(-₀)+πр_г². Следовательно, вблизи максимума в зоне электрон имеет отрицательную циклотронную массу т_н= — т*, т. е. движется как дырка. Эта ситуация наблюдается в случае почти заполненной зоны.

Ниже будет показано, что характер орбиты электронов в магнитном поле имеет большое значение для кинетических свойств электронов   (особенно   это   проявляется   в сильных магнитных полях).

4.2. Кинетика электронов с учетом магнитного поля

Кинетические свойства твердых тел оказываются сильно зависящими от наличия магнитного поля. При этом, как правило, различают две группы явлений: гальваномагнитные, связанные > с переносом заряда в магнитном поле, и термомагнитные, связанные с переносом энергии. В приближении времени релаксации кинетическое уравнение (3.4) имеет вид

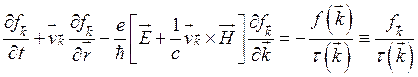                   (3.140)

Наличие в уравнении (3.139) члена 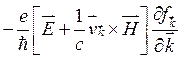 не позволяет, как сейчас будет  показано, заменить в этом члене   функцию   распределения     на   равновесную

Действительно,   заменяя f-» на !₀(е) и подставляя  в член с магнитным полем, получаем

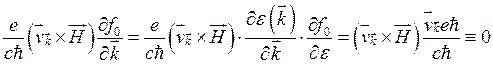 (3.141)

Таким образом, для равновесной функции распределения fo(e) магнитное поле никакого эффекта не дает. Дело в том, что при этом все носители вращаются вокруг направления поля без изменения энергии, поэтому на равновесные носители магнитное поле не оказывает влияния. Другое дело, если электроны участвуют в каком-либо потоковом движении с неравновесной функцией распределения. В этом случае магнитное поле изменяет направление движения носителей в потоке, тем самым меняя неравновесную часть функции распределения (в некотором смысле действие магнитного поля аналогично механизму рассеяния носителей). Следовательно, влияние магнитного поля должно учитываться неравновесной частью  функции распределения ,где  В этом случае вместо (3.139) получаем

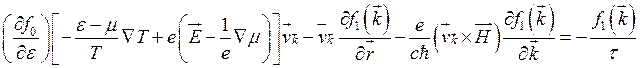   (3.140)’