Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 15

При рассеянии на примесях последние, как отмечено выше, можно считать шариками с сечением σ~а_в². Используя выражение τ(ε), получим

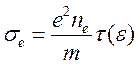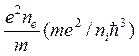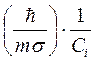~~, С_i=n_i/n_e,

(3.42)

где n_i—концентрация примесных атомов (отметим, что приводимая оценка справедлива как для нейтральных, так и для заряженных примесей). Учитывая, что σ ~ a_В² ~ /m²e⁴ ~ ~10^-16 см², получаем

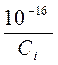                   ~   c^-1           (3.43)

Рассеяние па примесях упруго,  поэтому из   закона   Видемана—Франца имеем

σ_e~Т, эрг/(см∙с∙К).             (3.44)

                                                           Рассеяние на  фононах

Рассмотрим опять два случая рассеяния на коротковолновых и длинноволновых фононах.

1. Высокие температуры (k_BT >>). Для этого случая было найдено, что τ_ep~/k_BT. Отсюда получаем

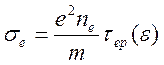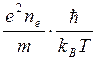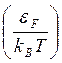~~~10¹⁶ с^-1

 (3.45)

Поскольку k_BT >>, то при рассеянии электронов на коротковолновых фононах изменение энергия ~k_BT/ε_F, т. е. оно мало и справедлив закон Видемана — Франца

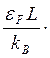~10¹⁶;   эрг/(см-с-К).

(3.46)

2. Низкие температуры (k_BT <<).. При рассеянии на длинноволновых фононах, как мы видели τ_ep~(/k_BT)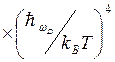,                      Поэтому электропроводность есть

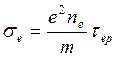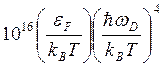~~c^-1

(3.47)

Следовательно, при рассеянии электронов на фононах при низких температурах имеет место соотношение σ_e~Т^-5, носящее название закона Блоха. 'Интересно, что можно получить, этот закон, пользуясь диффузионным приближением. Действительно, поскольку импульс электрона .порядка p_F ~ ~, то при T<<θ_D электрону нужно много раз столкнуться с фононами, чтобы потерять импульс порядка ~p_F. Из-за малого изменения импульса электрона его движение в импульсном пространстве можно считать диффузией (сравни с условием применимости диффузионного .приближения) вблизи поверхности Ферми. Поэтому величину τ можно получить из выражения для коэффициента диффузии в импульсном пространстве. Коэффициент диффузии (см. выше) есть среднеквадратичное изменение импульса за время порядка времени столкновения в данном случае с фононами, т. е. , где τ_ep^-1 — частота столкновений с фононами. Выше показано, что τ_ep^-1  пропорционально числу фононов, т. е. τ_ep~T³. Из соотношения Эйнштейна, имеющего в данном   случае   вид   p_F²≈D_pτ_ep

,   и   из   оценки ~

, сразу получаем τ_ep~T^-5, что ведет к закону Блоха.

Теперь оценим теплопроводность для этого вида рассеяния. Имеем

λ_e=clv_F~cv_F²τ_e~~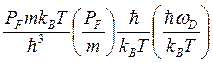

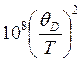
Таким образом, отношение λ_e/σ_e, есть

~

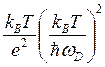
Следовательно, при низких температурах за счет столкновений электронов с длинноволновыми фононами закон Видемана—Франца нарушается, что связано с неупругостью таких процессов.

Рассеяние электронов электронами

Поскольку при межэлектронном рассеянии ~ то получаем

σ_е~~~~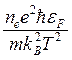

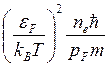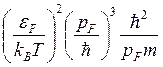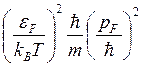
Но ~λ_в~10^-8 см (длина волны де Бройля—λ_е), ~1

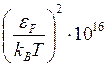σ_e~~ c^-1

λ_e~10^-8σ_eT~~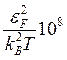

Относительно полученных формул сделаем следующее замечание. Рассмотренный тип рассеяния электронов на электронах приводит к существованию сопротивления, что не сов сем очевидно по следующим причинам. Для того чтобы су ществовало сопротивление, необходимо, чтобы полный им пульс электронов изменялся. Рассеяние электронов на элект ронах сохраняет полный импульс, поэтому, казалось бы электроны не должны испытывать сопротивления. Однако следует помнить, что на самом деле электроны имеют не истинный импульс, а квазиимпульс, определенный лишь с точностью до вектора обратной решетки. Следовательно, возможны процессы, приводящие к изменению полного импульса электронов. Эти процессы, как и в случае фононов, являются процессами переброса. Подробнее с их ролью в электронно-электронном рассеянии можно познакомиться в [8].

Для иллюстрации проведенных выше вычислений на рис. 3.2 приведены зависимости σ_е , λ_еи λ_е/σ_е для Сu как функции температуры.

Теперь посмотрим, каково соотношение между различными механизмами рассеяния я их вкладами в кинетические коэффициенты. Прежде всего укажем, что ял* удельного сопротивления установлено эмпирическое правило Матиссена

ρ=∑ρ_i= ρ₁+ρ₂           (3-52)