Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 27

Уже, исходя из перечисленных свойств поведения поперечного магнетосопротивления ясно, что его измерение может быть использовано для определения геометрии поверхности Ферми (подробнее см. [8, 14]). Ниже дается качественное объяснение указанных особенностей в поведении гальваномагнитных свойств. Полная кинетическая теория таких свойств в сильном магнитном поле является достаточно сложной и громоздкой и здесь изложена быть не может (ом. [13, 14]).

Обратимся к простому варианту гальваномагнитных явлений в сильных полях в рамках двухзонной модели (рассматриваются электроны в зоне проводимости и дырки в валентной зоне для полупроводников или электроны над поверхностью Ферми и дырки под ней для металлов). Сразу отметим, что в излагаемой модели не удается объяснить все особенности гальваномагнитных явлений, в частности, влияние открытости орбит на поперечное Магнетосопротивление. Поэтому наряду с результатами двухзонной модели будем привлекать качественные соображения и некоторые результаты кинетического рассмотрения.

Пусть имеются два типа носителей: электроны с концентрацией п ,и дырки с концентрацией р. Согласно [5],для двух типов носителей имеем

             (3.154)

где — соответственно проводимость и постоянная Холла. При  из (3.154) получаем

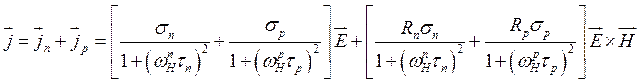   (3.155)

Теперь для простоты положим, что и дырми, и электроны имеют одинаковые эффективные массы и времена релаксации . Кроме этого, в силу противоположности зарядов электронов и дырок имеем , . Заметим, что сделанные нами упрощения не меняют качественной картины в поведении гальваномагнитных свойств. С учетом сказанного из (3.155) получаем

              (3.156)

где — проводимость в нулевом поле  . Если теперь в  (3.156)   выразить   через    и , то можно получить

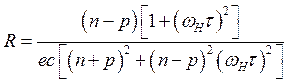  (3.157)

Проанализируем выражение  (3.157).   Если   п=р,   то R=0. Если , то

в слабых магнитных полях ()

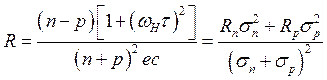         (3.158)

в сильных магнитных полях ()

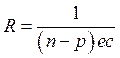_.                  (3.159)

Последний результат справедлив, как показывает строгое кинетическое рассмотрение [14], лишь в случае замкнутых орбит, причем (некомпенсированный материал). Исходя из (3.159), можно по величине постоянной Холла определить основной тип носителей в материале: электроны, если п>р, или дырки, если п<р. В случае .замкнутых орбит и компенсированного материала (п=р) имеем R~const. Для случая открытых орбит в направлении, перпендикулярном  имеем R~const [14]. Таким образом, характер зависимости Rдля замкнутых орбит в компенсированных материалах и для открытых орбит одинаков.

Рассмотрим теперь магнитосопротнвление в двухзонной модели. Ограничимся случаем поперечного магнетосопротивления (продольное магнетосопротивление в двухзонной модели, как можно показать, вообще отсутствует в силу изотропности этой модели). По определению, магнетосопротивление есть

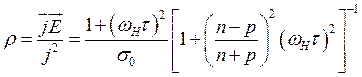                 (3.160)

или для  получаем

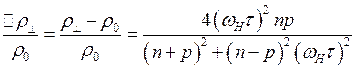                   (3.161)

При  (слабые магнитные поля)   из  (3.161)   получаем

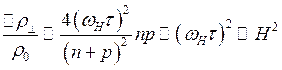   (3.162)

Этот случай, как отмечалось выше, подтверждается на опыте в случае слабых магнитных полей. Далее, с увеличением ω_н τ величина Δρ/ρ₀ замедляет рост и наконец при  насыщается, т. е. перестает зависеть от величины магнитного поля (такое поведение, как отмечено выше, также наблюдается экспериментально):

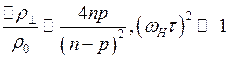.               (3.163)

Формула (3.163), однако, имеет место лишь для некомпенсированных веществ, у которых . При п=р из (3.161) получаем

.                 (3.164)

Последнее соответствует случаю слабых магнитных полей (3.162).

Приведенное рассмотрение, как показывает строгий анализ [14], справедливо лишь для замкнутых орбит в магнитном поле, когда столкновения вообще не оказывают влияния на магнетосопротивление.

В случае существования открытых орбит дело обстоит сложнее. Важнейшим свойством твердых тел с открытыми поверхностями Ферми является резкая анизотропия этих поверхностей, т. е. геометрия таких поверхностей зависит от направления. Именно анизотропия поверхности Ферми приводит к возможности при определенных направлениях магнетосопротивлению возрастать неограниченно, при других—насыщаться. Для иллюстрации рассмотрим пример какой-нибудь открытой поверхности Ферми. Пусть для простоты это будет гофрированный цилиндр (напомним, что <в силу периодичности решетки поверхности Ферми (открытые) также периодичны и продолжаются в импульсном пространстве по всей обратной решетке). В этом случае, если магнитное поле перпендикулярно оси цилиндра, орбиты открыты и носители могут двигаться неограниченно; если не перпендикулярно, орбиты оказываются замкнутыми (см. рис. 4.3). Уже на этом