Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 19

Подвижность носителей и электропроводность

Будем  рассматривать собственный  полупроводник, в котором   концентрации   электронов   и   дырок   равны    (п=р).

Функции распределения каждого .из носителей и определяются из Кинетического уравнения (3.5). При этом нетрудно получить

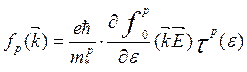                                                   (3.87)

(напомним, что заряд дырки противоположен заряду электрона).

Аналогично случаю с одним типом носителей (см. выше), вычислим плотности тока:

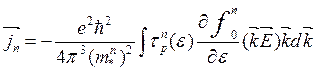                                                        (3.88)

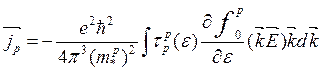                                                  (3.88)   

Рассмотрим сначала электроны. Если полупроводник невырожден (как здесь предполагается), то энергия электронов может отсчитываться от дна зоны проводимости. Тогда в соответствии с результатами первой части пособия имеем (в первой части концентрации электронов и дырок обозначались соответственно N_e, и N_e).

                                              (3.90)

где  — эффективная   плотность   состояний в зоне проводимости.

Используя (3.90), Получаем

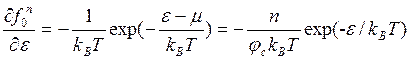                                                  (3-91)

Подставляя (3.91) в (3.88), имеем

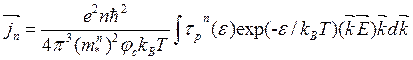.                                (3.92)

Пользуясь соотношением [6]

получаем

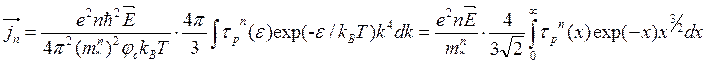        (3.93)

где  x=. Вводя обозначение

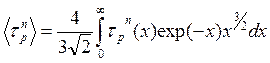(3.94)

имеем из (3.93)

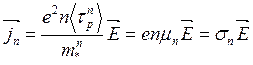                                                  (3.95)

Здесь    σ_n— электропроводность     электронов  - их   подвижность.   Соответственные    вычисления для дырок дают

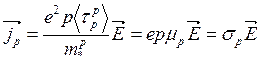                                                       (3.96)

где

Полная плотность тока есть

                                                          (3.97)

Поскольку подвижность непосредственно связана (как и проводимость) с временем релаксации, то вес определяется механизмами рассеяния. В частности, температурная зависимость подвижностей носителей может быть определена, если известны τ^p и τⁿ. Практически во всех случаях имеет место соотношение где А_pn— константы, слабо зависящие от температуры. Пользуясь табл. I и выражениями для μⁿ и μ^p, можно получить, например, и случае рассеяния на акустических колебаниях

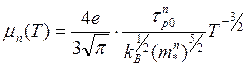                                                                                              (3.98)

Или при рассеянии на примесных ионах:

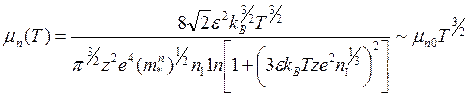                   (3.99)

Таким образом, подвижность падает с температурой, если носители рассеиваются, в основном, на акустических фононаж и растет, если рассеяние происходи! па примесных ионах. Напрлмер, в Ge: T≈300 К; μ_n ≈ 0.38м²/(В·с);           μ_n(Т = 77К) ≈ 3.7 м²/(В·с); μ_p(Т = 300К)  ≈ 0.18м²/(В·с); μ_p(Т = 77К) ≈ 4.4 м²/(В·с).          Хорошо видно, что при высоких температурах подвижность электронов выше подвижности дырок, а при низких — наоборот. Интересно рассчитать проводимость собственного полупроводника при комнатной температурe и сравнить с приводимостью  примесного полупроводника.  Рассмотрим  случай   Ge  при    Т=300 К.   Оценки   дают φ = = 4,8·10²¹ Т^3/2 м^-3      (принято,     что m_n*= m_p* = m).   N_e, = N_e = 2,5·10²⁵  м³;   n = p=3,l • 10¹⁹.    При этом σ=en(μ_n + μ_p) =2,8 1/(Ом·м). Теперь оценим σдля Ge, тегированного  ионнлозаннымп    примесными    атомами  с  концентрацией    ~10²⁰  м^-3.   В этом   случае   оценки   дают   σ ~ б.7 0м·м.  Таким образом,  проводимость Ge при легировании возрастает более чем .в два раза.