Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 26

Кроме возникновения эффекта Холла (появления холловского поля под некоторым углом к направлению тока) во внешнем магнитном поле изменяется также и составляющая тока j_x(например, для случая рис. 1.16). Последнее означает, что сопротивление тела изменяется. Эксперименты показывают, что для слабых магнитных полей относительное удельное сопротивление  подчиняется соотношению (его можно получить и расчетным путем в случае слабых магнитных полей — см. например, [5, 12]):

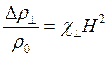   (3.151)

где ; величина  носит название коэффициента поперечного магнетосопротивления. Эта величина зависит от физических свойств тела. Поясним эффект магнетосопротивления исходя из уравнения (3.143), полагая j_y =j_z ==0, Е_z = 0 и исключая поле Е_z. В этом случае, как нетрудно показать

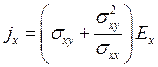     (3.152)

Следовательно,   в  поперечном   поле   Н электропроводность равна

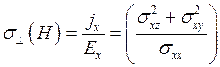    (3.153)

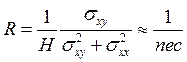
Зная компоненты σ_ik, можно найти коэффициент х_х. Если магнитное поле параллельно току, т. е. Н=Н_Х, то  и . Для слабых магнитных полей приведем окончательные результаты (случай одного типа носителей) вычисления постоянной Холла и компонент магнетосопротивления  [6]:   (3.154)

            ;         (3.154)

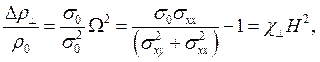
Таким образом, как показывает опыт и простейшая теория, в слабых магнитных полях поперечное магнетосопротивление неограниченно растет с ростом магнитного поля . Выше, однако, нигде не было указано, что следует понимать под слабостью поля. Довольно ясно, что магнитное поле может быть охарактеризовано ларморовским циклотронным радиусом , а носители — длиной свободного пробега l.  Если , то можно считать, что столкновения разрушают ларморовское вращение и магнитное поле слабо сказывается на движении зарядов. Указанный критерий можно также записать в виде , где ω_н — циклотронная частота, τ_e — время релаксации. В случае  (слабые магнитные поля) магнетосопротивление определяется искривлением траекторий в магнитном поле на величину приблизительно . Других причин изменения сопротивления нет. При этом, естественно, характер электронных траекторий (геометрия поверхности Ферми) мало сказывается на магнетосопротивлении.

Сильные поля

В сильных полях (или ) гальваномагнитные эффекты имеют ряд особенностей. Дело в том, что в сильных магнитных полях столкновения редки, так что носители могут либо описывать за время между столкновениями сложную траекторию по замкнутой орбите, определяемой условиями ε=const, p_z=const (при замкнутых поверхностях Ферми  или для отдельных траекторий на открытой поверхности Ферми), либо совершать неограниченное движение по открытой орбите (в случае открытых поверхностей Ферми). В том и другом случаях характер движения определяется геометрией изоэнергетической поверхности и ее ориентацией по отношению к направлению магнитного поля (подробный разбор всех возможных вариантов имеется в [13, 14]). Кроме этого, гальваномагнитные свойства определяются соотношением концентраций носителей (см. ниже).

Указанные особенности гальваномагнитных свойств продемонстрируем на поведении поперечного магнетосопротивления . При этом экспериментально наблюдаются следующие три случая:

1.  Магнетосопротивление  может достигать насыщения т. е. , причем . В этом случае насыщение имеет место всегда,   вне зависимости   от   ориентации магнитного поля относительно осей кристалла   (расположения .поверхности Ферми относительно направления магнитного поля). Указанное поведение поперечного магнетосопротивления экспериментально обнаружено у Al, Na, Li и т. д. (эти элементы имеют замкнутую поверхность Ферми).

2.  Магнетосопротивление  растет при сколь угодно больших магнитных полях и для любых   ориентаций   кристалла (эго наблюдается у Bi, Sb, W, Mo и т. д., особенностью которых является одинаковая концентрация электронов в зоне проводимости и дырок в валентной зоне),

3.  Магнетосопротивление   в некоторых   направлениях может обнаруживать насыщение,   а при близких   к ним направлениях может расти неограниченно с ростом поля. Такое поведение обнаруживается у Сu, Ag, Аu, для которых характерно наличие открытых орбит на поверхности Ферми.