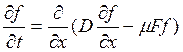Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 5

                                                                                                       (1.38)

В равновесном стационарном состоянии из (1.38) имеем

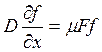
Боли сила Fпотенциальная, т. е. F=—dU/dx, то получаем

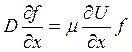                                                                                                                    (1.39)

Отсюда

f(х)=Сехр(—μU//D).                                                      (1.40)

С другой стороны, в состоянии равновесия имеет место распределение Больцмана f=Cexp(—U/k_BT).. Следовательно, получаем

                                              (1.41)

Формула  (1.41)  носит   название   соотношения Эйнштейна и связывает коэффициент подвижности с коэффициентом диффузии. Это соотношение будет использовано ниже при изучении кинетики полупроводников. Заметим также, что используя (1.41), ток j_x можно записать в виде

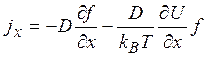(1.42)

Отсюда сразу следует, что в однородном электрическом поле U=eExимеет место соотношение

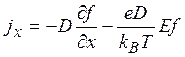                              (1.43)

Следовательно, ток состоит из диффузионной (—Ddf/dx) и дрейфовой (—eDEf/k_BT) частей. Произведя осреднение функции распределения в импульсном пространстве, используя

Соотношение п=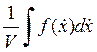, получим выражение для плотности макроскопического тока 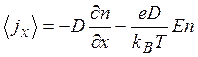                                                                                                                            (1.44)

Аналогичное соотношение, ее т ест в они о, имеет место и в трехмерном случае.

2. КИНЕТИКА ФОНОННОЙ ПОДСИСТЕМЫ ТВЕРДОГО ТЕЛА

Рассмотрев общие вопросы физической кинетики, обратимся теперь к изучению конкретной подсистемы твердого тела — фононам. Напомним, что квазичастицы фононы — это элементарные возбуждения в кристаллической решетке, связанные с волнами смещений групп атомов. С фононами в состоянии термодинамического равновесия мы познакомились в первой части настоящего пособия (см. [7, 8]). Здесь изучим кинетику фононов с учетом их взаимодействия между собой — фонон-фононные взаимодействия, появляющиеся при учете в потенциальной энергии взаимодействующих атомов членов кубических и более высокой степени в разложении по степеням смещений из положений равновесия, а также с другими квазичастицами. Отметим, что в большей части изложение будет носить качественный характер без использования сложных математических методов (с последними можно ознакомиться в [2, 7]).

Изучение кинетики фононов необходимо прежде всего потому, что они ответственны за тепловое сопротивление диэлектриков и некоторых полупроводников. Кроме этого, поглощение звука в диэлектриках в значительной степени связано с фононами. С точки зрения эти основных задач и будут в дальнейшем рассматриваться вопросы кинетики фононов.

2.1. Кинетическое уравнение для фононов

Изучение кинетики фононов проводится согласно общему методу, изложенному в главе I. Прежде всего необходимозаписать вероятности перехода фононов между различными состояниями, составить интеграл столкновений и поставить его в правую часть уравнения Больцмана.

Отметим, что в ряде случаев нужно рассматривать не сами фононы, а составленные из них волновые пакеты. Однако в дальнейшем будем считать, что всю кинетику можно излагать на языке отдельных фононов и их взаимодействий, пренебрегая указанным обстоятельством (этот вопрос подробно изложен, например, в [7]). Напомним, что в кристаллах со сложной решеткой (больше одного атома па элементарную ячейку) существует два типа ветвей колебаний решетки и, следовательно, два типа фононов — акустические и оптические, причём всего имеется три акустические ветви и (Зs-3) оптических (s—число атомов в элементарной ячейке) ветвей. В связи с этим функцию распределения фононов удобно записать для каждой ветви спектра  описывающую плотность  числа   фононов   ветви   Кинетическое уравнение тогда будет иметь вид

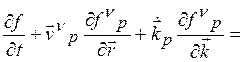
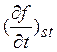                      (2.1)

Здесь скорость фонона  ветви есть 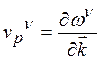, a = . Интеграл столкновений в правой части уравнения (2.1) должен включать процессы столкновения фононов (как одной, так и разных ветвей спектра) и взаимодействие фононов с другими квазичастицами и нарушениям; идеальности решетки — дефектами, границами отдельных монокристаллов, границами твердого тела и т. д. Суммируя все сказанное, можно формально записать