суммарный
вектор, например ![]() +
+![]() =
-
=
- ![]() , лежит вне
данной элементарной
ячейки (.содержащей векторы
, лежит вне
данной элементарной
ячейки (.содержащей векторы ![]() и
и ![]() ). Но свойства кристаллов эквивалентны во всех элементарных ячейках (см. первую часть пособия). Если
же часть суммарного вектора
). Но свойства кристаллов эквивалентны во всех элементарных ячейках (см. первую часть пособия). Если
же часть суммарного вектора
![]() +
+![]() вышла за данную ячейку, то из закона сохранения энергии фононов
вышла за данную ячейку, то из закона сохранения энергии фононов ![]() +
+![]() =
=
![]() (справедливого внутри каждой ячейки) следует, что нужно «вернуть» суммарный вектор
(справедливого внутри каждой ячейки) следует, что нужно «вернуть» суммарный вектор ![]() в исходную ячейку. Таким образом,
нужно «перебросить»
вектор
в исходную ячейку. Таким образом,
нужно «перебросить»
вектор ![]() в
«свою» ячейку. В связи с этим процессы, протекающие при условии (2.4), носят
название процессов
переброса (или U-процессов). Заметим,
что несмотря на
то, что выбор элементарной ячейки в кристалле неоднозначен, для всех ячеек
в
«свою» ячейку. В связи с этим процессы, протекающие при условии (2.4), носят
название процессов
переброса (или U-процессов). Заметим,
что несмотря на
то, что выбор элементарной ячейки в кристалле неоднозначен, для всех ячеек ![]() нельзя обратить в нуль (хотя всегда можно выбрать отдельные ячейки так,
чтобы в ник
нельзя обратить в нуль (хотя всегда можно выбрать отдельные ячейки так,
чтобы в ник ![]() =0).
=0).
Аналогичная ситуация имеет место и для процессов рассеяния фононов более высокого порядка (четырехфононных и т.д. (см. [7,8])).
2.2. Теплопроводность решетки
Применить указанные выше методы для изучения теплопроводности решетки здесь не представляется возможным, поскольку они являются весьма громоздкими. Однако проведенное выше качественное рассмотрение кинетики фононов позволит разобраться b механизмах теплопроводности решетки.
В целом ряде кристаллов с малым числом электронов (или дырок): диэлектриках, полуметаллах, некоторых полупроводниках — теплопроводность полностью определяется теплопроводностью решетки. Ниже дается простейшая теория теплопроводности решетки, основанная на приближении длины (или времени) свободного пробега фононов.
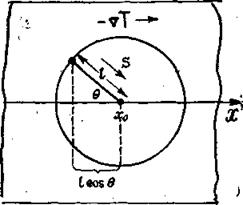
Рис: 2.2
Получим сначала выражение для коэффициента теплопроводности решетки
исходя из феноменологических представлений. Рассмотрим в кристалле некоторую малую
область вблизи
точки х0 (рис. 2.2). В эту точку приходят фононы, которые испытали последнее столкновение на
длине, не большей, чем lp. В каждой точке
твердого тела поток энергии можно записать в виде
![]() , где
, где ![]() — средняя скорость
фононов в точке
— средняя скорость
фононов в точке ![]() ; ε(
; ε(![]() )—их характерная энергия е этой точке (напомним, что, согласно
распределению Планка число фононов в окрестности данной точки определяется температурой вблизи нее).
Пусть для простоты, рассматривается, во-первых, элементарная ячейка с одним
атомом (простая), во-вторых, для всех ветвей справедлив закон дисперсии ω = сsk. Найдем средний поток
энергии вдоль оси х, если вдоль нее действует заданный градиент температуры
(рис. 2.2):
)—их характерная энергия е этой точке (напомним, что, согласно
распределению Планка число фононов в окрестности данной точки определяется температурой вблизи нее).
Пусть для простоты, рассматривается, во-первых, элементарная ячейка с одним
атомом (простая), во-вторых, для всех ветвей справедлив закон дисперсии ω = сsk. Найдем средний поток
энергии вдоль оси х, если вдоль нее действует заданный градиент температуры
(рис. 2.2):
![]() (2.5)
(2.5)
Здесь осреднение ведется по
телесному углу θ. Примем, что энергия ε в точке ![]() определяется
температурой Т (
определяется
температурой Т (![]() ), т. е ε
(Т (
), т. е ε
(Т (![]() )). Поскольку в точку х0 поступает энергия лишь из сферы радиусом lp, то
)). Поскольку в точку х0 поступает энергия лишь из сферы радиусом lp, то
![]() =
= 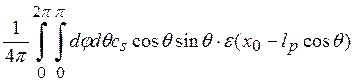 =
= 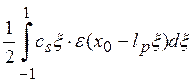
разложим ![]() в ряд
в ряд
![]() =
=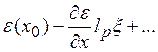 (2.7)
(2.7)
Учитывая лишь линейный градиент температуры
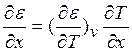 , получим из (2.6) и
(2.7)
, получим из (2.6) и
(2.7)
![]()
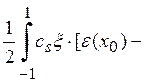
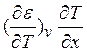
![]() ]dξ = -
]dξ = - 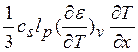 =
- λ
=
- λ![]() (2.8)
(2.8)
Таким образом, имеем
![]() -
- 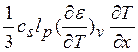 = - λ
= - λ![]() (2.9)
(2.9)
Здесь Cv=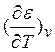 и λ =
и λ =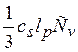 — соответственно теплоемкость
и теплопроводность. Окончательно, для коэффициента теплопроводности фононов или решетки получаем
— соответственно теплоемкость
и теплопроводность. Окончательно, для коэффициента теплопроводности фононов или решетки получаем
λP =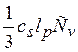 (2.10)
(2.10)
Следовательно, как и в
кинетике разреженного газа, коэффициент теплопроводности решетки определяется
характерной скоростью ![]() , длиной свободного пробега фононов lPи теплоемкостью Cv. Для расчета необходимо
вычислить указанные величины. Оценка
, длиной свободного пробега фононов lPи теплоемкостью Cv. Для расчета необходимо
вычислить указанные величины. Оценка ![]() может быть получена
из рассмотрения спектра фононов, величина Cvвычислена по методу,
разобранному
в первой части пособия. Следовательно, основная трудность состоит в вычислении длины
свободного пробега lP. Как видно из выражения
для интеграла столкновений (2.2), для получения разумных величин lР следует учитывать в общем случае все
механизмы рассеяния. Рассмотрим последовательно «клад различных механизмов в
величину lP, а следовательно, — в решеточную
теплопроводность.
может быть получена
из рассмотрения спектра фононов, величина Cvвычислена по методу,
разобранному
в первой части пособия. Следовательно, основная трудность состоит в вычислении длины
свободного пробега lP. Как видно из выражения
для интеграла столкновений (2.2), для получения разумных величин lР следует учитывать в общем случае все
механизмы рассеяния. Рассмотрим последовательно «клад различных механизмов в
величину lP, а следовательно, — в решеточную
теплопроводность.
Начнем со случая чистого монокристалла достаточно больших размеров. При этом следует выделить следующие предельные случаи:
1. Низкие температуры (Т<<θD).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.