Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 31

где ,  - соответственно эффективные плотности состояний в зоне проводимости и в валентной зоне. Из (5.16) видно, что с повышением температуры величина работы выхода уменьшается. Интересная закономерность наблюдается в полупроводниках n- или p-типа. Пусть ф_д, ф_а — эффективтные плотности состояний атомов-доноров и соответственно атомов-акцепторов (первые приводят к проводимости n-типа,  вторые — к р-типу) . Тогда работы выхода соответственно есть

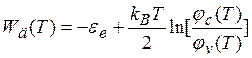                  (5.17)

W_a ( Т) 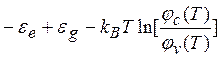.            (5. 18)

Из (5.17) и (5.18) видно, что работа выхода электронов из дырочного (р-типа) полупроводника значительно выше, чем у полупроводника электронного (n-типа — порядка энергии запрещенной зоны). На рис. 5.5а, б показаны соответствующие энергетические зоны (рис. 5,5,а — n-тип.рис. 5.5,6 — р-тип).

5.3. Автоэлектронная (холодная) эмиссия

Вполне понятно, что если даже температура тела близка к нулю, т. е. термоэлектронная эмиссия отсутствует, прикладывая значительное внешнее электрическое поле, можно изменить условия на потенциальном барьере и заставить электроны проходить сквозь этот барьер. Отметим, что в принципе возможна ситуация, когда за счет прикладываемого внешнего поля при T=0 высота барьера становится равной уровню химического потенциала (энергии Ферми для металлов) и даже меньше его. Такой эффект, как можяо показать, проявляется в очень сильных внешних полях E*>10⁸ В/см (он носит название эффекта Шоттки и не является квантовым явлением). Однако в реальных условиях заметная эмиссия при T == 0 наступает уже в полях E~10⁷ В/см, что нельзя объяснить эффектом Шоттки. Оказывается, поселение тока в этом случае связано с возможностью туннелирования электронов сквозь потенциальный барьер, высота и ширина которого сильно зависят от поля. Подобный вид электронной эмиссии называется холодной или автоэлектронной.

Рассмотрим автоэлектронную эмиссию металлов. Геометрия задачи аналогична рассмотренной в случае термоэмиссии. Внешнее электрическое поле пусть направлено перпендикулярно плоскости yOz— поверхности твердого тела (в отрицательном направлении оси х, поскольку только в этом случае электроны будут двигаться из тела в вакуум — см. рис. 5.6).

Прежде всего запишем потенциал, действующий вблизи поверхности на электроны. Учтем, что в суммарном потенциале  можно оставить лишь два члена (учет других слагаемых, связанных с более точной аппроксимацией барьерного потенциала, не приводит к заметным изменениям результатов): потенциал —хЕ, связанный с действием внешнего электрического поля Е,  и потенциал =1/4x, вызванный силами зеркального изображения. Последний потенциал связан с тем, что при удалении электрона от тела на расстояние х внутри тела на расстоянии х от поверхности индуцируется положительный заряд, создавая силу F_s=e²/4x², не дающую, электрону свободно уйти в вакуум (выражение для такой силы можно записать при х>а, где а—межатомное расстояние). Таким образом, согласно сказанному, можно написать (см. рис. 5.6) для потенциальной энергии V=e:

V(x) =e= - W, х<0;

V(x) = - e²/4x - eEx, х>а.(5.19)

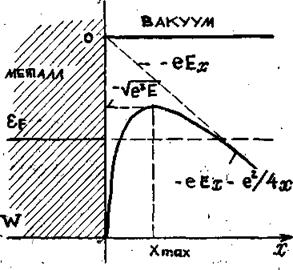
Рис. 5.6

При х>а можно из  (5.19)  вычислить  величину максимума V_тахи его положение x_тах. Вычисления дают

V_тах=  ,  x_тах =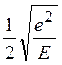                                                                                      (5.20)

Отметим, что на рис. 5.7 штриховой линией показан потенциальный барьер, не учитывающий сил зеркального изображения. Наличие потенциального барьера конечной ширины и высоты приводит, как следует из квантовой механики [3, 4], к конечной вероятности прохождения потенциального барьера (тунелированию) даже в случае ε_F <V_тах. Здесь не будет проводиться соответствующего решения уравнения Шрединтера c потенциалом (5.19); отметим только, что, когда на длине волны электрона λ_В ~2π/k потенциал V(x)

ме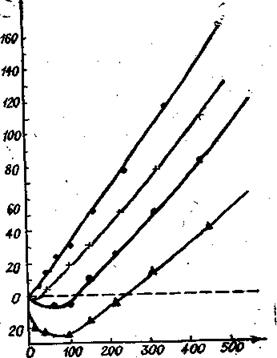

Рис. 5.7

меняется слабо, решение может быть получено в квазиклассическом приближении (методом ВКБ) (см. [8, 16]). При этом волновая функция внутри потенциального барьера есть

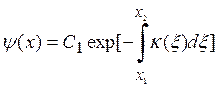                                                      (5.21)

Здесь 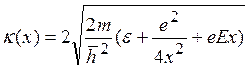; х₁, х₂ — значения координаты х, в юторых к(х) обращается в нуль. Плотность тока эмиссии есть