Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 17

Из выражения (3.70) видно, что плотность тока определяется не только электрическим >полем, но и градиентом температуры. Вычислим в случае металлов величину р*_е (с учетом зоммерфельдоэвской поправки):

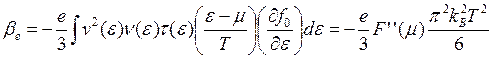
При   получении    (3.72)     были    использованы    разложения 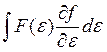 (см.     (3.33)),     причем 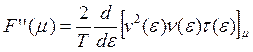, Следовательно, имеем

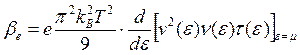
Пусть теперь плотность тока равна нулю: , тогда из (3.70) получаем

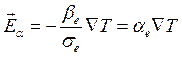
Таким образом, в твердом теле под действием градиента температуры возникает электрическое поле Е_а, которое носит название. термоэлектрического, а величина а_е называется дифференциальной термо-ЭДС. Вычислим последнюю чину. Имеем

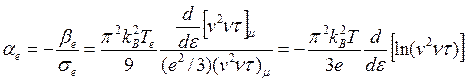
Оценим α_е для газа свободных электронов. Имеем , т (е) ~ ; тогда (u²VT) ~2е,т//л²А³. Следовательно, получаем

Таким образом, для таза свободных электронов дифференциальная термо-ЭДС отрицательна и является очень малой величиной (при этом для T~10^-3 и ~10³ К/см имеем

Е_α~10^-2 В/см). Для реальных металлов величина а_е может быть довольно сложной функцией температуры, при этом может даже менять знак (по сравнению с моделью газа свободных электронов (см. [8, 13])). На рис. 3.4 показана зависимость α_e(T) для чистых образцов Сu.

Выше был рассмотрен эффект появления электрического поля в твёрдом теле под действием градиента температуры. Аналогичным образом можно найти дополнительный вклад в поток тепла под действием электрического поля  и т.д. В общем случае  и  можно записать в виде [2, 13].

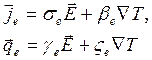                                  (3.77)

При этом существует определённая связь между коэффициентами   и . Если ввести величины ρ_е=σ_е^-1, α_е= β_е/σ_е, λ_е=γ_еβ_е/σ_е – ς_е, то из (3.77) получаем

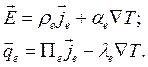                                  (3.78)

Причём γ_e =-β_eT,  откуда Π_e=α_eT, λ_e=-(Tβ_e²/σ_e+ς_e). Эти соотношения будут использованы ниже при рассмотрении конкретных термоэлектрических эффектов. Укажем, что коэффициенты в (3.77) или (3.78) могут быть выражены в изотропном случае через коэффициент дифференциальной термо-ЭДС α_е, вывод которого дан выше.

Обратимся теперь к конкретным термоэлектрическим явлениям, имеющим важное практическое значение.

Эффект Зеебека

Рассмотрим разомкнутую цепь (рис.3.5,а), состоящую из двух проводников, между которыми находится третий проводник. При этом свойства проводников 1 (см. рис.3.5,а) одинаковы. Пусть в точках а и bтемпература одинакова, а в точках c и d – разная Т_с = Т₁, Т_d = Т₂, Т_a = Т_b = Т₀.

Поскольку  из (3.77) имеем  (α_e=-β_e/σ_e). Разность потенциалов между точками      a и bназывается термоэлектродвижущей силой:

                                                       (3.79)

Таким образом, в неоднородно нагретом проводнике возникает термо-ЭДС, величина, которой пропорциональна разность температур горячего и холодного участков тела. Это явление называется эффектом Зеебека. Заметим, что величина  определяется также разностью дифференциальных термо-ЭДС двух проводников. На эффекте Зеебека основан принцип действия термоэлементов, для которых соотношение (3.79) обычно записывают в виде , причём величина          α₁₂~(α₂ - α₁) определяется природой полупроводников термоэлемента и интервалом температур. Важно, что поведение α₁₂ может значительн меняться с температурой и даже менять знак.

Эффект Пельтье

Теперь рассмотрим контакт двух различных проводников, находящихся при постоянной температуре (рис. 3.5, б). При  из соотношений (3.78) имеем: 

                                                                                                    (3.80)

Величина Π_e=α_eT, поэтому в одномерном случае q_e=α_eTj_e. Для значений по обе стороны контакта имеем

q_e׀_l²= -j_eT(α₂ - α₁)                                                                                                              (3.81)

Здесь учтено, что температуры и плотности потоков по обе стороны контакта непрерывны. Из (3.81) следует, что в отсутствие градиента температуры есть поток тепла, связанный с выделением (или поглощением) тепла на контакте (3.81). Это тепло называется теплом Пельтье. А величина   П₁₂=T(α₂ - α₁) - коэффициентом Пельтье. Таким образом, при протекании через контакт тока в нём выделяется тепло, пропорциональное первой степени плотности тока (Эффект Пельтье). Тепло Пельтье есть Q_T=q_eS (S – площадь контакта). Заметим, что эффект Пельтье меняет знак при изменениизнака (направления) тока, т.е. тепло может выделяться и поглощаться.