Возникший таким образом д-войной электрический слой и 'Порожденное им электрическое поле препятствуют выходу других электронов из тела, т. е. на поверхности тела возникает потенциальный барьер для электронов φn. На рис. 5.2,а показано распределение потенциала внутри и вне тела, а на рис. 5.2,6—аппроксимация этого распределения.
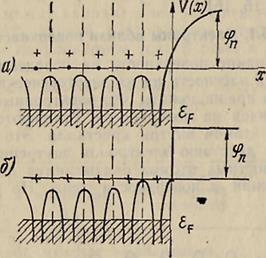
Рис. 5.2
Рассмотрим теперь вопрос о том, как наличие потенциального барьера на поверхности влияет на волновые функции и энергетический спектр электронов. Важно отметить, что качественное поведение волновых функций электрона вблизи поверхности слабо зависит от аппроксимации потенциального барьера, поэтому можно использовать простейший его вид.
Вне твердого тела, если энергия электрона не превышает высоты потенциального поверхностного барьера, волновая функция электрона должна экспоненциально убывать по мере удаления от поверхности тела [8]. В плоскости поверхности тела волновая функция должна быть периодической, согласно теореме Блоха. Пусть поверхность тела совпадает с плоскостью уОz, а нормаль к ней — с осью х. Тогда полная волновая функция электрона может быть записана в виде [8]
(5.1)
где
(5.2)
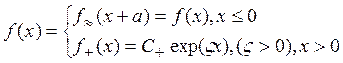
Здесь а —
«вектор» решетки; 
)—периодическая функция
с периодом решетки в направлении оси х. Энергетический спектр электронов .в этом случае можно
представить в виде
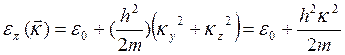(5.3)
где ε0 — энергия в запрещенной зоне внутри кристалла. Вид волновых функции (5.1) и (5.2) и спектр (5.3) носят название поверхностных или таммовских состояний, причем f(x) — локализованная вблизи поверхности тела волновая функция, отвечающая энергии ео в запрещенной зоне. Локализация волновой функции на поверхности обязана простой физической причине: со стороны вакуума движение электрона ограничено наличием потенциального барьера, а со стороны кристалла — дифракцией электронной волны па кристаллическом потенциале, которая запрещает распространение электрона вглубь кристалла при определенных значениях его энергии (область запрещенных состояний). На рис. 5.3 изображена
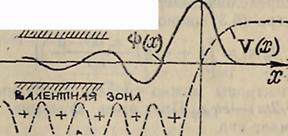
Рис. 5.3
указанная ситуация {сплошная линия—волновая функция поверхностного состояния, локализованная вблизи поверхности и затухающая экспоненциально в запрещенной зоне, штриховая линия—потенциальная энергия электрона у поверхности кристалла [15]).
Для целого ряда .кинетических явлений, связанных с поверхностными электронами, важно привлечение правильного выбора нуля отсчета энергии. Поскольку во всех расчетах термодинамических и кинетических характеристик фигурирует лишь разность энергий, следует определять выбор нуляотсчета их физических соображений. Будем считать, что φ=0 (рис. 5.2,6) соответствует свободному электрону вне тела. Электроны внутри тела удерживаются притяжением ионов, поэтому для удаления электрона из тела нужно затратить энергию, равную — εF. Выбрав за нуль энергию, равную энергии свободного электрона, Нужно считать уровень Ферми εF отрицательным. При этом все остальные уровни энергии (заштрихованные на рис. 5.2.6) расположены еще ниже. Понятно, что при наличии потенциального барьера φп на границе твердого тела полная энергия, которую следует затратить на извлечение электрона с уровня Ферми и равная ширине потенциального барьера, вычисляется как
(5.4)
Энергия 
, обозначаемая часто как W, носит название работы выхода. Здесь нет возможности
описать более строгие подходы к изучению поверхности и поведению вблизи нее электронов (например,
чрезвычайно интересный вопрос о (влиянии магнитного поля на поверхностные
состояния электронов). С ними можно ознакомиться в [5, 8, 15]. Теперь обратимся к
статистике электронов вблизи поверхности. Функция распределения электронов вблиз
поверхности
есть распределение Ферми—Дирака и с учетом энергетического спектра (5.3)
записывается в виде
(5.5)
Вне тела
электроны можно считать свободными и для них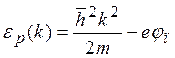 
. При этом функция
распределения (5.5) принимает вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.