Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 3

Запишем функцию распределения в виде

=+                                                    (1.16)

Здесь— равновесная функция распределения; — малая неравновесная добавка к  (|| << ||). Если система выведена из состояния термодинамического равновесия неслишком сильным возмущением, то  в большинстве случаев можно записать в виде

[2, 6]:

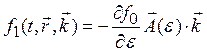                                                       (1.17)

где 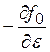    — функция,  зависящая    от  ε     (скалярная); — векторная, функция, зависящая от ε. Тогда можно записать

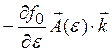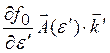 - =  - +  (1.18)

Если рассеяние упругое, то из  (1.18)  получаем  (ε=ε'):

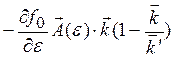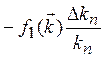 - = =                                                              (1.19)

Здесь  = (-)_n; k_n, k_n^’ — проекции и  иа вектор . Подставляя (1.19) в (1.4) с учетом (1.9), получаем

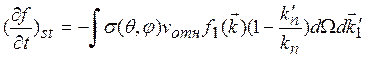                                                                                                (1.20)

Нетрудно видеть, что интеграл, на который умножается функция f₁ (), имеет размерность обратного времени. Поэтому вводят величину τ (), называемую временем релаксации, согласно соотношению

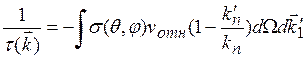                                     (1.21)

Таким образом, получаем

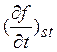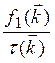=                                                                                                (1.22) 

Запись интеграла столкновений в виде (1.22) и называется приближением времени релаксации. В дальнейшем именно это приближение .будет использовано для вычисления (кинетических .коэффициентов твердого тела. Еще раз отметим, что при этом были сделаны лишь два предположения: а) рассматриваемые состояния являются слабонеравновесными; б) рассеяние квазичастиц упруго. Нарушение любого из условий, указанных выше, приводит к существенному усложнению описания кинетики процессов в твердом теле (см., однако, следующий раздел). Для ознакомления с методами изучения  кинетических  явлений,  не описываемых в  рассматриваемых здесь рамках, можно обратиться к [6, 8].

Выражение для     можно записать в виде, удобном для его оценок, через эффективное сечение рассеяния. Для этого   выберем    направление   вдоль   .   Тогда   =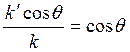 так как .   Следовательно, получаем

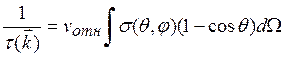(1.23)

Величина

                                                                                     (1.24)

носит название транспортного сечения рассеяния. Таким образом, можно написать

(1.25)

Для N рассеивающих центров соответственно получаем

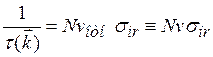(1.26)

При этом длина, на которой происходит релаксация импульсов, есть

l()=τ()v = Nσ_ir.   (1.27)

Отметим, что в силу   во всех рассмотренных выше формулах можно  заменить на ε, т. е. τ(ε) = [Nvσ_ir]^-1. Аналогичные выражения получаются для других соотношений. Приведенные формулы удобны для оценок величин τ() и l(). Ниже будут привешены конкретные их выражения для различных механизмов рассеяния.

В заключение    раздела поясним    еще    раз качественно   смысл τ-приближения. Пусть рассматривается неравновесное однородное   состояние   системы   квазичастиц   в   отсутствие внешних полей. Тогда кинетическое уравнение в т-приближении, исходя из (1.2) и (1.22), будет иметь вид

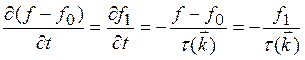                                                                                                   (1.28)

Отсюда получаем

                                                                                           f(t) = f₀ + Cexp(-t/τ)                                                                                                        (1.29)

где С определяется начальными условиями (неравновесным распределением при t = 0). Таким образом, слабонеравновесное состояние, описываемое функцией f, релаксирует к равновесию с функцией f₀ за время τ, которое определяет время этого процесса. Важно, что процесс такого возвращения к состоянию равновесия зависит от энергии (или импульса) и вообще говоря, различен для разных неравновесных состояний, Конкретные примеры применения                      τ-приближения будут рассмотрены ниже при изучении кинетики различных подсистем твердого тела.

1.5. Диффузионное приближение (уравнение Фоккера—Планка)