Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 12

Более строгий анализ показывает, однако, что время свободного пробега (релаксации) зависит от энергии носителей [6]:

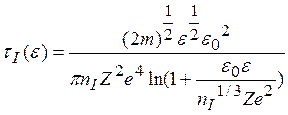~                                                                             (3.8)

Здесь п_I— концентрация заряженных лримесей. Таким образом, при рассеянии на заряженных примесях ~ε^3/2 имеет степенной вид в зависимости от энергии: =. При малых энергиях ε→0 из (3.8) получаем

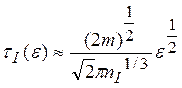~                                                                                   (3.9)

т.е. =.

Рассеяние на фононах

Рассеяние электронов на фононах представляет собой до^: вольно сложный процесс, причем сечение последнего сильно зависит от типа фононов: акустические или оптические. Здесь мы проведем лишь оценки сечения таких .процессов и вычислим время релаксации электронов на фононах. Точные методы вычисления сечения электрон-фононного рассеяния можно найти в [5, 6, 13].

Удобно рассмотреть два предельных случая — коротковолновых и длинноволновых фононов   (пренебрежем   здесь тем обстоятельствам, что в сложной решетке могут быть два типа ветвей-акустические и оптические). Два указанных пре дельных случая соответствуют высоким и низким температурам решетки.

1. Пусть k_BT>>ω_D (высокие температуры). Тогда электроны поглощают и излучают фононы с энергией порядка ω_D. Поскольку T>>θ_D, то из распределения Бозе—Эйнштейна число фононов в этом случае f_p ~ k_sT/ω_D. Для вероятности рассеяния W(см. [5, 13]) получаем

W~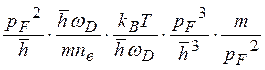~                                                              (3.10)

Здесь использовано, что n_e~р³/; Из (3.10) следует, что

~~                                       (3.11)

2. При k_BT<<ω_D основную роль играют фононы с энергией ω ~k_BT. При этом энергия электронов заметно изменяется в каждом акте рассеяния (случай неупругого рассеяния). В этом случае вероятность рассеяния можно оценить из выражения  [13]

W~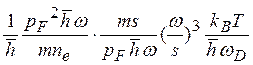~ ()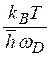²                                             (3.12)

где s— скорость фонона  (s=ωq); кроме того, попользованы соотношения  ω/s~ k_BT/s, ω~k_BT, p_Fs~ k_BT

При рассеянии электронов   на длинноволновых фононах угол рассеяния есть [13] θ~q/p_F~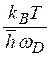<<1например, [6]). Время релаксации при θ<<1 равно

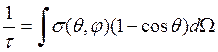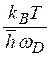 ~ ()⁴                                                                                                                    (3.13)

Рассеяние электронов электронами

Рассеяние электронов друг на друге происходит аналогично рассеянию электронов на заряженной примеси, поскольку кулоновский потенциал взаимодействующих электронов заэкранирован в твердом теле. Отсюда ясно, что радиус межэлектронного взаимодействия .порядка межатомного расстояния. Оценим изменение импульса при рассеянии. Из соотношения неопределенности в области взаимодействия электронов имеем ΔрΔr~ или Δр~/Δr. Выше видели, что Δr~/mv_e. Таким образом, Δр ~ mv_e ~р. Следовательно, иэменение импульса при рассеянии порядка самого импульса. Теперь оцеиим изменение энергии электрона при рассеянии. Пусть электрон в состоянии рассеивается на электроне , т. е. имеет место процесс +=+ . Из-за принципа

Паули число частиц порядка k_ВT/ε_F, а частиц — k_ВT/ε_F (это определяется числом свободных мест). Следовательно, вероятность рассеяния W~n_e(k_BT)²/ε_F, где п_е — концентрация свободных электронов. Для времени релаксации τ_ee~W^-1, где W~ (k_BT)²/ ε_F, получаем

                                                               τ_ee~ ε_F / (k_BT)²~ 10^-5 / (k_BT)², с(3.14)

Здесь использовано, что τ_ее-~l_е/v_F~а_в(ε_F /(k_BT))². Подчеркнем, что электронно-электронное рассеяние является н супругам: энергия при рассеянии меняется на величину порядка Δε~р².

3.3.  Электропроводность  и электронная  теплопроводность

Обратимся теперь к вычислению электропроводности твердого тела и вкладу электронов в теплопроводность. Оба этих процесса переноса будем определять в слабонеравновесном состоянии, описываемом функцией распределения . Последняя, согласно проведенным выше рассуждениям, подчиняется кинетическому уравнению Больцмана (3.5).

Рассмотрим сначала поведение электронов во внешнем электрическом поле, причем будем считать, что =0. В этом случае из (3.5) получаем (H=0)