Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 23

Рассмотрим прежде всего характер траектории, следующий из (3.126). Запишем решение (3.126) в форме . Тогда сразу видно, что движение в пространстве импульсов равномерное. Из закона сохранения энергии ε()—е= =const следует, что

                 (3.127)

Поскольку для свободного электрона в кристалле ε()— периодическая функция (а значит, ограниченная), то из (3.127) следует, что траектория электрона в координатном пространстве является ограниченной. Действительно, из (3.127) имеем Δr_E = Δε/еE, где r_E— координата электрона вдоль направления поля Е; Δε — ширина энергетической зоны, в которой находится электрон. Можно показать, что вдоль определенных осей в кристалле электрон в поле Е совершает периодические колебания с периодом [14]:

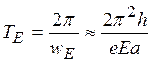                                                                                                            (3.128)

где ω_E=2еЕ/Δр_E — частота колебаний электрона   в поле E;

Δр_E —период функции ε() вдоль поля E (Δр_E = h/a; а — межатомное расстояние). Размер орбиты электрона при этом есть r_E~v_FT_E. Оценим Т_к и r_E  Для металла с проводимостью σ_e ~10⁸, Ом∙см^-1, при разумных полях Е~10^-6 В/см (при этом плотность тока j_e ~10^-2A/см²) получаем  ~10~²-0.1 c^-l, r_E ~ 10⁶---10⁷ см. Таким образом, квазиэлектрон в постоянном электрическом поле имеет орбиту размером r_E >>l_e (l_e — длина свободного пробега). Следовательно, в реальных условиях невозможно наблюдать ограниченность электронной орбиты, поскольку она разрушается столкновениями на длине l_e. Электрон при этом двигается в поле почти прямолинейно, имея положительное или отрицательное ускорение в зависимости от знака эффективной массы т,.

Теперь обратимся к динамике электрона в магнитном поле, которое будем считать однородным (электрическое поле при этом отсутствует). В этом случае имеем

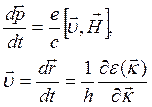              (3.129)                                         

Уравнение (3.129) аналогично уравнению движения свобод-нон заряженной частицы в магнитном поле. Однако существенное отличие для электрона в кристалле состоит в том, что v (k)  есть сложная периодическая функция k, определенная его законом дисперсии е(#). Последнее обстоятельство приводит к ряду важных физических следствий.

Будем рассматривать теперь всю обратную решетку, а не ограничиваться одной зоной Брнллюэна. Такой подход удобен при рассмотрении динамики электронов в магнитном поле. При этом энергия е является сложной периодической функцией р или k. В дальнейшем   будем   называть поверхность e(/>)=const иэознергетической. В частности, поверхность Ферми относится к нзоэнергетическим поверхностям (напомним, что поверхность Ферми — граничная поверхность е(/))=е_у, внутри которой при Г=0 все электронные состояния заняты, а вне — свободны).

Динамика электрона в магнитном поле зависит от геометрии поверхности Ферми e(p)=e_f. При этом все поверхности Ферми могут быть двух типов:

а) замкнутые — в пространстве обратной решетки имеется периодически повторяющаяся поверхность (внутри одной зоны Бриллюэна такая поверхность нигде не подходит к границе зоны); на рис. 4.1,я схематически показаны такие поверхности (.в реальных условиях замкнутые Поверхности ми ц.меют AI, Bi, W, Li, Na, Mo);

б) открытые — в обратной решетке такие поверхности непрерывно повторяются {в одной зоне Бриллюэна такие поверхности всегда подходят к границам), схематически открытая поверхность показана на рис. 4.1,6 (поверхности такого типа имеют, например, Fe, Аи, Сэ, Си).

Возвращаясь к уравнению  (3.129), получаем для случая

= (О, О, Н)

(3.130)

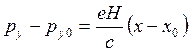
При этом имеют место равенства

                  (3.131)

Итак, согласно (3.131), электрон движется таким образом, что у него сохраняются ε л р_z.                В импульсном пространстве это соответствует траектории, получающейся при пересечении поверхности ε()=constплоскостью р_z = consl. Для металлов, как известно, основную роль играют электроны с энергией ε< ε_F, поэтому важную роль играют сечения поверхности Ферми плоскостью p_z=const. Вполне понятно, что если поверхность Ферми замкнутая, то все ее сечения являются замкнутыми кривыми, а если она открытая, то сечения могут быть как открытые, так и замкнутые. Важно отметить, что из уравнений (3.130) и (3.131), а также из уравнений