Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 10

Рассмотрев частотную зависимость коэффициента поглощения звука, обратимся теперь к его температурной завиоимости. Оценим вначале вклад теплопроводности в γ^Т и получающуюся отсюда зависимость γ(Т). Поскольку вклад теплопроводности существенен лишь для продольных волн и из (2.22) имеем γ^Т ~ 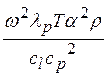,-Toпри T>>θ_Dполучаем, что γ^Т не зависит от температуры (поскольку, как видели выше, λ_P ~ Т^-1.). При T<<θ_D  λ_P ~exp()., а следовательно, γ^Т является экспоненциально убывающей функцией температуры — затухание за счет теплопроводности.

Для оценки влияния вязкости на температурную зависимость γ поступим следующим образом. Прежде всего заметим, что вязкостное поглощение звука на языке фононов означает следующее. Звуковая волна, поглощение которой рассматривается, имеет длину волны значительно большую, чем длины волн колебаний решетки (тепловых фононов), находящейся в равновесии. Следовательно, при прохождении звука по кристаллу он изменяет незначительно период решетки, причем на расстояниях, превышающих постоянную решетки. Но дисперсия фононов (см. первую часть пособия) зависит от периода решетки, поэтому в присутствии звука зависимость  меняется. Это приводит к изменению скорости фононов, входящих в кинетическое уравнение (2.1). Тем самым возникает неравновесность в фононной подсистеме, которая будет уменьшаться за счет взаимодействия фононов. Таким образом, релаксируя к состоянию равновесия, система взаимодействующих фононов забирает энергию у звуковой волны • (отметим, что состояние равновесия в кристалле соответствует случаю отсутствия звуковой волны). Проведенное качественное рассуждение показывает, что в рассматриваемом случае необходимо кинетическое рассмотрение. Такое рассмотрение дает для температурных зависимостей вязкостного затухания (γ^в — затухание за счет вязкости)

γ^в ~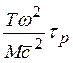, T>>θ_D

γ^в ~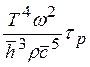, T<<θ_D

Здесь М — масса атома в решетке; 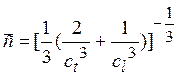      — средняя скорость звука в кристалле (см. первую часть пособия); - время релаксации фононов. Для проведения оценок необходимо знать зависимость (T), которую можно получить из следующих соотношений: ~ l_p/~ λ_P/c_v. При T>>θ_D, λ_P ~ Т^-1 имеем (T)~ Т^-1, т. е. при высших температурах γ^в зависит, как и теплопроводностная часть, от температуры. В случае T<<θ_Dоценка более сложная [2] и дает γ^в ~ω²/T.

Поскольку γ= γ^Т + γ^в, то можно утверждать, что при низких температурах γ^Т>>γ^в (γ^Т убывает экпоненциально с температурой, а γ^в — степенным образом), т. е. процессы теплопроводности дают более значительный вклад в поглощение звука. Для иллюстрации полученных выше зависимостей на

На рис 26 приведена зависимость γ(Т) Для свинца: кривая 1— продольный звук, со,/2л~26,3 МГц; кривая 2 — поперечный, м₍/2я~10,1 МГц.

В случае распространения коротковолнового звука процесс затухания есть результат рассеяния отдельных фононов  (описывающих звуковую волну)   тепловыми   фононами. При этом получается следующая зависимость [2]:

γ ~ωТ⁴                                                    (2.25)

Таким образом, для коэффициента поглощения коротковолнового звука .имеет место линейная зависимость от частоты.

3. КИНЕТИКА ЭЛЕКТРОННОЙ ПОДСИСТЕМЫ

Обратимся теперь к изучению кинетических явлений, связанных с электронной подсистемой твердого тела. Изучение кинетики электронной подсистемы важно прежде всего потому, что позволяет исследовать процессы электропроводности и электронной теплопроводности, а также влияние Электронов на затухание звука ib твердом теле. Особый интерес представляет также поведение электронов в магнитном поле и связанные с этим кинетические эффекты. Этому кругу вопросов в основном и 'посвящена данная глава.

3.1. Кинетическое уравнение для электронов

Прежде всего на основании общих принципов физической кинетики получим кинетическое уравнение для электронов в твердом теле. Напомним, что электроны, являясь квазичастицами, имеют закон дисперсии ε(). Зная закон дисперсии, можно определить скорость электрона к