Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 8

Если газ фононов достаточно разрежен, т. е. выполняется неравенство (это соответствует кнудсеновскому случаю в кинетике разреженного газа)

d<<l_N, l_v(2.11)

где l_N, l_v— соответственно длины свободного пробега за счет нормальных процессов и процессов переброса, d— характерный размер  образца, то в формулу (2.9) следует подставить величину d:

λ_P =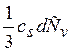                                       (2.12)

При низких температурах зависимость C_V(T) имеет вид (cм. первую часть подобия)                          C_V(T) ~const(T/θ_D)³, откуда

                                                    λ_P =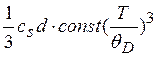~  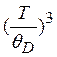                                         (2.13)

Следовательно, теплопроводность решетки в этих условиях полностью определяется поведением C_V(T). Оценим теперь «клад нормальных процессов и процессов переброса. Пусть в кристалл поступает с границы некий поток тепла (на языке фононов это соответствует движению фононов с некоторым полным импульсом 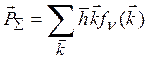 ). Однако, как мы видели, в нормальных процессах квазиимпульс сохраняется. Таким образом, нормальные процессы приводят лишь к перераспределению энергии и квазиимпульса между отдельными фононами, но не приводят к уменьшению суммарного квазиимпульса. Итак, нормальные процессы не могут привести к конечному тепловому сопротивлению решетки. Это очень важный результат, говорящий о том, что Даже ангармоничность кристалла (если сохраняется суммарный импульс) не может привести к конечному значению теплопроводности.

Обратимся теперь к процессам переброса, в которых суммарный импульс не сохраняется. В процессах переброса суммарный импульс все время разрушается, тем самым как бы изменяется направление передачи энергии. Этим процессы переброса создают (конечное тепловое сопротивление. В чистых монокристаллах больших размеров (напомним, что рассматривается случай кристаллов с малым числом электронов или дырок) процессы переброса являются единственным механизмам, обеспечивающим конечное тепловое сопротивление. Оценим температурную зависимость l_v. В случае трехфононного процесса =++; для осуществления последнего необходимо, чтобы хотя бы один фонон был длинноволновым (это можно показать, учитывая, что из условия (2.4) следует: какой-либо  должен быть величиной порядка  Пусть этим, вектором будет, например, . Тогда из ~k_Bθ_D и закона сохранения энергии += следует, что и ~k_Bθ_D. При Т<<k_Bθ_D из планковского распределения получаем

f_P() ~ exp(-),              f_P() ~ exp( -),           

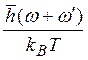f_P() ~ f_P()f_P() ~ exp( -)~ exp( -)~ exp( -)

где β — коэффициент порядка единицы. Следовательно, при низких температурах число процессов переброса экспоненциально мало (этим и объясняется возможность кнудсеновского случая d<<lv). Поскольку lv~f_P^-1, lv~exp( ). Принимая степенную зависимость для C_V(T) при T<<θ_D, по лучаем                        ,                     \

λ_P = exp( ).                               (2.14)

2.  Промежуточные температуры T≤θ_D

В этом случае можно осуществить условие lv~d²/l_N, тогда λ_P будет определяться формулой (2.14) [7].

3. Высокие температуры T>>θ_D

При высоких температурах f_P~ Максимальное значение энергии системы фононов есть k_Bθ_D. Таким образом, при T>>θ_D  энергия всех фононов 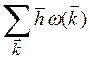<< причем ~ k_Bθ_D. . Теплоемкость при T>>θ_D следует закону Дюлонга —Пти, отсюда получаем

λ_P =const Т^-1.                                (2.15)

Здесь использовано, что T>>θ_D lv~f_P^-1. Таким образом, при высоких температурах теплопроводность решетки обратно пропорциональна температуре (закон Дебая).

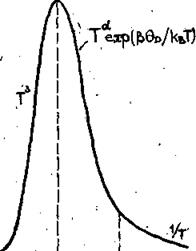
⁰   _ ^     \ ..Т

Рис. 2.3

Суммируя изложенное, на рис. 2.3 построена зависимость λ_P(Т) в широкой области температур. При T<T₁λ_P(Т) ~ Т³ при T₁<T<T₂λ_P(Т) ~ exp( ); при T<T₂  λ_P ~Т^-1.. На рис. 2.4 приведены реальные зависимости для ряда веществ: кривая 1 — сапфир (Аl₂О₃), кривая 2— алмаз (С).