Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 18

Эффект Томсона

Найдем теперь изменение энергии единицы объема проводника в единицу времени с учетом термоэлектрических эффектов. Такое изменение равно потоку энергии из объема и выделению (-или поглощению) энергии в объеме, т. е.

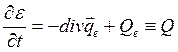
Последний член в (3.82) связан с работой электрического поля и равен . Таким образом, имеем . Используя соотношения (3.78), получаем

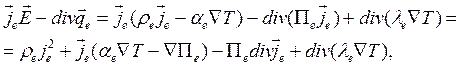   (3.83)

где . Если div , то

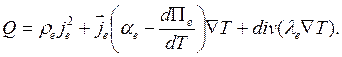(3.84)

Поскольку Π_e=α_eT, α_e - dΠ_e/dT=TdΠ_e/dT, следовательно:

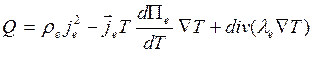(3.85)

Величина χ=TdΠ_e/dT называется коэффициентом Томсона. Тепло носит название тепла Томсона. Таким образом в неоднородном проводнике наряду с выделением джоулева тепла р,/Д пропорционального квадрату плотности тока л переноса тепла теплопроводностью, существует тепло Томсона Q_T . Это явление называется эффектом Томсона. Поскольку эффект Томсона пропорционален первой степени плотности тока, то он может менять знак: в неоднородно нагретом проводнике тепло Томсона может и выделяться и поглощаться в зависимости от направления тока. Заметим что для реальных проводников коэффициент Томсона сильно зависит от температуры и может даже менять знак.

3.5. Кинетика носителей в полупроводниках

До сих пор изучалась кинетика процессов в твердом теле, когда имелись носители одного знака — электроны. Однако, как отмечалось в первой части пособия, наряду с носителями в зоне проводимости — электронами — при термическом, например, возбуждении полупроводника появляются носители положительного знака в валентной зоне—дырки. В силу этого обстоятельства кинетика полупроводников становится сложнее кинетики металлов. Прежде всего отметим здесь простейшие свойства полупроводников, важные с точки зрения их кинетики.

Во-первых, носители тока в полупроводниках могут быть либо вырожденными (тогда их кинетика близка к кинетике металлов), либо невырожденными (тогда в ряде простейших случаев их кинетика схожа с кинетикой газовой плазмы).

Во-вторых, следует различать собственные (без примесей) полупроводники; в них при термическом возбуждении число электронов в зоне проводимости всегда равно числу дырок в валентной зоне. Не следует забывать, однако, что эффективные массы обоих носителей могут сильно различаться, т.е. m_*ⁿ≠m_*^p (в этой части .пособия индексом п обозначены электроны, индексом р — дырки). Кроме этого, имеются «примесные (иначе, легированные) полупроводники: в них числа электронов .ц дырок могут сильно отличаться [6]. В зависимости от вида примеси в полупроводнике может наблюдаться либо преимущественно электронная проводимость (полупроводники n-типа), либо дырочная (полупроводники р-типа).

В-третьих, наличие двух типов носителей приводит к двум законам дисперсии е„(А) и е_р(Ј), что также усложняет ситуацию по сравнению со случаем металлов. Ниже, как правило, будем считать законы дисперсии простейшими — квадратичными и изотропными (более сложные случаи — см. [6]).

Время релаксации носителей в полупроводниках

Кинетику полупроводников будем рассматривать в приближении времени релаксации. Для удобства приведем здесь выражения для времен релаксации импульса т_р(е) и энергии т«(е) для носителей (здесь подразумевается преобладание какого-либо типа носителей, т. е. полупроводники относятся либо к п-, либо р-типу). В большинстве случаев эти времена можно записать в степенном виде

τ_p(ε)=τ_p0(T)ε^r, τ_ε(ε)=τ_ε0(T)ε^q                                                                                   (3-86)

где rи q—некоторые .константы, а функции τ_p0(T) и τ_ε0(T) ~ A_iT^β, где A=const; β—показатель (подробно ознакомиться с расчетом подобных выражений для разных механизмов рассеяния можно в [6]). В табл. 1 приведены конкретные выражения в зависимости от механизмов рассеяния носителей (некоторые из этих -выражений были получены ранее нами при рассмотревши механизмов рассеяния). В этой же таблице приведены для примера данные для слабоионизованной плазмы. Обсуждение указанных зависимостей проводить не будем (см., например, [6]), укажем лишь, что в кинетику полупроводников вклад электронно-дырочного рассеяния почти всегда мал.

Таблица 1