Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 14

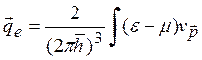
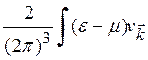
 =                                                                                      (3.31)

Заметим, что здесь под интегралом стоит величина (ε—μ), а не е, как можно было бы ожидать. Поясним это обстоятельство. Дело в том, что истинный поток тепла, связанный с теплопроводностью, обычно определяется в отсутствие электрического тока. Поэтому из полного потока энергии электронов следует вычесть поток свободной энергии электронного газа, связанный с переносом химического потенциала μ. Используя выражение (3.30), получим

     (3.32)

Для взятия интеграла в формуле (3.32) следует воспользоваться для металлов и вырожденных полупроводников тем же приемом, каким пользовались при расчете электропроводности. Однако использование соотношения (∂f₀/∂ε)=-δ приводит к обращению выражения (3.32) в нуль. Следовательно, нужно учитывать температурные (зоммерфельдовские) поправки вблизи ε≈μ, как это делалось в первой части пособия (см. также [8]). С учетом следующего члена разложение (∂f₀/∂ε)есть [8]:

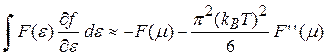        (3.33)

Используя (3.33), получаем из (3.32)

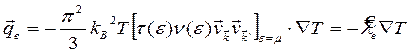 (3.34)

Если q_e‌‌‌‌||, то  (в общем   случае,   величина представляет собой тензор теплопроводности, которая становится скаляром в изотропных телах и кубических кристаллах). Отсюда получаем

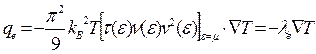     (3.35)

Таким образом, получена линейная связь между градиентом температуры и потоком тепла, носящая' название закона Фурье.

Проведем   оценки   величин   σ_е и λ_e, для газа   свободных электронов. В этом случае имеем (см. первую часть пособия) ν(ε)=ν(ε_F)=(2m³ ε)^1/2 /π², v(μ)=v(ε)=v_F Отсюда получаем (v_F=ε_F^1/2/m^1/2):

        (3.36)

     (3.37)

Число электронов в единице объема есть n_e=2V_F/(2n)³, где V_F=(4/3)πp_F³ -объем сферы Ферми. Следовательно, имеем

                (3.38)

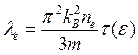                                                    (3.39)

Таким образом, получаем   хорошо   известные соотношения для электронных коэффициентов переноса.

Получим теперь соотношение, связывающее  величины σ_е и λ_е. Из  (3.38)  и (3.39)  имеем

Соотношение (3.40) носит название закона Видемана—Франца, а постоянная L = π²k_в²/3е² называется постоянной Лоренца; ее значение есть L = 2,45 ∙10^-8 Вт∙Ом∙К^-2. Для реальных металлов при Т=373 К отношения λ_e/σ_еТ имеют следующие значения: Ag—2,37∙10^-8 Вт∙Ом∙К^-2, Мо—2,79∙10^-8 Вт∙Ом∙K^-2.

В ряде веществ может наблюдаться заметное расхождение величин Lи λ_e/σ_еТ, что обусловлено механизмами рассеяния. Поясним это. Характерное время потери импульса τ_p(ε) (время релаксации импульса) в ряде ситуаций может заметно отличаться от характерного времени потери энергии τ_ε(ε) (время релаксации энергии). Например, такая ситуация имеет место при неупругом рассеянии электронов: энергия при неупругом рассеянии изменяется сильно, в то время как импульс — незначительно (конкретный пример такого процесса будет указан ниже). При этом следует отметить, что в общем случае величина электропроводности определяется временем релаксации импульса τ_p(ε), а электронная теплопроводность — временем релаксации энергии τ_ε(ε)

В  этом    случае   отношение    λ_e/σ_е,    принимает   вид    (l_ε~τ_evl_p~τ_pv):

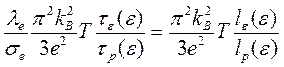                                 (3.41)

Тем самым, если τ_ε≠τ_p, то всегда закон Видемана—Франца будет нарушаться. При упругих столкновениях время релаксации импульса τ_p и время релаксации энергии примерно равны (поскольку в этих процессах энергия и импульс по абсолютной величине сохраняются, только меняется направление импульса, приводящее к тому, что функция распределения становится изотропной). Поскольку одним из условий применимости τ -приближения есть условие упругости процессов рассеяния, то в этом приближении всегда имеет место закон Видемана—Франца. Подчеркнем, что последнее формально связано с использованием времени релаксации, являющимся единым как для рассеяния с потерей импульса, так и с потерей энергии.

Используя полученные выше выражения для времени релаксации, вычислим кинетические коэффициенты σ_е и  λ_e .

Рассеяние на примесях