Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 22

Таким образом, для низкочастотного звука при ql_e <<1коэффициент поглощения пропорционален квадрату частоты звука и длине свободного пробега электронов γ ~ ω². В противоположном предельном случае ql_e>>1, но ωτ_е <<1 вычисления дают следующий результат. Поглощение звука электронами эффективно лишь при выполнении условия       ≈ ω, т. е. в поглощении принимают участие лишь электроны, волновые векторы и скорости которых удовлетворяют указанному равенству. Поскольку ω ~ sq, то сosθ = s Следовательно, звук поглощают только электроны, движущиеся в фазе со звуковой волной. Это аналогично хорошо известному в физике плазмы затуханию Ландау. Отметим, что поскольку s/<<1, то cosθ ~ s/v_F<<1 я θ~π/2, т. е. электроны, которые поглощают энергию звуковой волны, движутся перпендикулярно к направлению ее распространения (волновому вектору ). Для величины Q_e рассчет дает Q=, поэтому

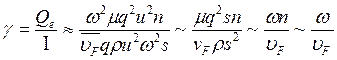                                   (3-122)

Здесь, как и в (3.120), μ — величина, характеризующая упругие константы металла. Выражение (3.122) показывает, что коэффициент поглощения в этом случае пропорционален первой степени частоты звуковой волны и не зависит от длины свободного пробега электронов.

2. Высокочастотный звук (ωτ_е >>1). Поглощение звука при условии ωτ_е >>1 нужно рассматривать, как и в случае поглощения звука фононами, как процесс испускания и поглощения отдельных фононов. При этом также возможны случаи ql_e>>1 и ql_e<<1.

В случае ql_e<<1 вычисления дают [14]

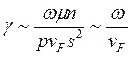                                                                             (3.123)

Последнее выражение   аналогично   случаю   низкочастотного звука при о)т_е<С1.

При ql_e<<1 поглощение звука происходит за счет электронов, движущихся фактически в однородном поле звуковой волны. Причиной поглощения в этом случае является вязкость электронного газа. Коэффициент поглощения в данном случае вычисляется так же, как и в обычном газе (ср. со случаем затухания звука за счет фононов) [2]:

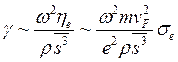
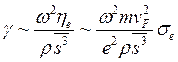                                                                (3.124)

где η_e - вязкость электронного газа; σ_e - его электропроводность. Например при низких температурах, как было показано было показано, 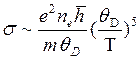  , где n – концентрация электронов. Отсюда получаем

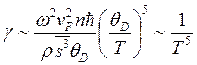                                                            (3.125)

Следовательно, при низких температурах вклад электронов в поглощение высокочастотного звука оказывается превалирующим.

Целый ряд важных и интересных явлений имеет место при распространении и поглощении звука в магнитном поле. С указанным кругом вопросов, а также с целым рядом других эффектов при распространении звука в твёрдом теле можно познакомиться в [13, 14].

4. КИНЕТИКА ЭЛЕКТРОНОВ В МАГНИТНОМ ПОЛЕ

Интересный класс кинетических явлений возникает при помещении твердого тела в магнитное поле. Из всего многообразия имеющихся здесь эффектов будут рассмотрены лишь динамика электронов в магнитном поле и гальваномагнитные явления. С другими вопросами кинетики носителей в магнитном поле можно подробно ознакомиться в [2,5, 12 - 14].

4.1. Динамика электронов в магнитном поле

Рассмотрим поведение электронов твердого тела в магнитном поле. Ограничимся  квазиклассической механикой электронов. Таким образом, эффекты, связанные с квантовыми свойствами электронов, включая влияние спина, здесь не затрагиваются. Им будет посвящено специальное рассмотрение (см. третью часть пособия). Следует отметить, однако, что рассмотрение электрона в твердом теле уже формально содержит квантовый подход, без которого невозможно определить закон дисперсии ε(). Вопросы поведения электронов, связанные с магнитными .свойствами твердых тел, будут рассмотрены в третьей части пособия.

Сначала рассмотрим квазиклассическую механику электронов с определенным законом дисперсии в постоянном и однородном электрическом поле. Уравнение движения в этом случае можно записать в виде

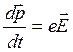                                                  (3.126)