![]() (
(![]() ) =
) =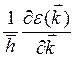 . Уравнение движения электрона есть
. Уравнение движения электрона есть
![]() (3.1)
(3.1)
или
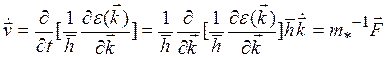
Здесь m*=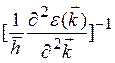 — эффективная масса электрона.
— эффективная масса электрона.
Вводя функцию
распределения для электронов ![]() и
воспользовавшись (3.2), можно
записать кинетическое уравнение Больцмана
и
воспользовавшись (3.2), можно
записать кинетическое уравнение Больцмана
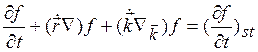
Во внешнем
электромагнитном поле на электрон действует сила Лоренца, ![]() , поэтому уравнение (3.3)
, поэтому уравнение (3.3)
приобретает
вид (![]() =
=![]() ):
):
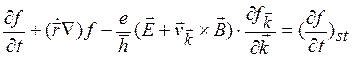 (3.4)
(3.4)
В дальнейшем нас
будут интересовать кинетические явления, происходящие недалеко от состояния
термодинамического равновесия. В этом случае удобно ввести функцию ![]() =
=![]() -
-![]() где
где ![]() — равновесная функция, распределения Ферми — Дирака. Имея
в виду изучение твердого тела, температура которого меняется от точки к точке
(состояние неполного или
локального термодинамического равновесия), введем
температуру Т (
— равновесная функция, распределения Ферми — Дирака. Имея
в виду изучение твердого тела, температура которого меняется от точки к точке
(состояние неполного или
локального термодинамического равновесия), введем
температуру Т (![]() ). При этом будем
полагать, что равновесная функция распределения Ферми — Дирака определяется локальной
температурой, т. е.
). При этом будем
полагать, что равновесная функция распределения Ферми — Дирака определяется локальной
температурой, т. е. ![]() =
= 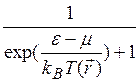 (подробное обсуждение
возможности такого вида
(подробное обсуждение
возможности такого вида ![]() можно найти, например, в [5, 6]). С
учетом сказанного уравнение (3.4) примет вид
можно найти, например, в [5, 6]). С
учетом сказанного уравнение (3.4) примет вид
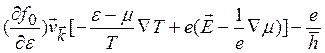 [
[![]() ]·
]·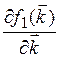 -
- 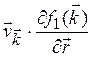 =
=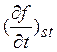 (3.5)
(3.5)
Заметим, что при
записи уравнения (3.5) опущен член вида 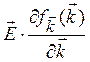 , нарушающий, как можно
показать [5, 6], закон Ома. Последний же считается справедливым всегда при не
слишком больших полях.
, нарушающий, как можно
показать [5, 6], закон Ома. Последний же считается справедливым всегда при не
слишком больших полях.
Полученное уравнение Больцмана для функции
f1(![]() ) является достаточно
сложным. Для получения обозримых результатов
воспользуемся (Приближением времени релаксации, которое обсуждалось в первой главе. В этом случае интеграл столкновений
) является достаточно
сложным. Для получения обозримых результатов
воспользуемся (Приближением времени релаксации, которое обсуждалось в первой главе. В этом случае интеграл столкновений
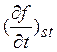 можно записать
через время релаксации τ(
можно записать
через время релаксации τ(![]() ). Отметим, что строгий анализ показывает, что величины, полученные в приближении
времени релаксации, достаточно
хорошо описывают экспериментальные зависимости, Поэтому для Электронов приближение времени релаксации широко используется (см. [5, 6, 13,
14]).
). Отметим, что строгий анализ показывает, что величины, полученные в приближении
времени релаксации, достаточно
хорошо описывают экспериментальные зависимости, Поэтому для Электронов приближение времени релаксации широко используется (см. [5, 6, 13,
14]).
Сделаем еще одно замечание. Процессы столкновений электронов с другими квазичастицами, а также с дефектами решетки практически всегда можно рассматривать как рассеяние на некотором силовом центре, состояние которого не изменяется. Так обстоит дело при рассеянии на нейтральных и заряженных примесях, фононах и т. д. Последнее обстоятельство позволяет получить в явном виде выражение для времени релаксации или его оценку.
3.2. Время релаксации электронов
Займемся вычислением времени релаксации для различных процессов рассеяния электронов.
Рассеяние на нейтральных примесях
Электрон взаимодействует с нейтральной примесью за счет наведенного
дипольного взаимодействия. Потенциал такого взаимодействия, есть V(r)=—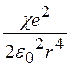 (дипольный момент равен
(дипольный момент равен ![]() =
= 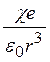 . Здесь χ — электрическая поляризуемость атома примеси,
. Здесь χ — электрическая поляризуемость атома примеси, ![]() — статическая диэлектрическая проницаемость.
Нетрудно видеть, что этот потенциал очень быстро спадает с расстоянием, поэтому можно
считать атом примеси
«шариком» размером приблизительно а0. Этот размер по величине равен боровскому радиусу аВ=
— статическая диэлектрическая проницаемость.
Нетрудно видеть, что этот потенциал очень быстро спадает с расстоянием, поэтому можно
считать атом примеси
«шариком» размером приблизительно а0. Этот размер по величине равен боровскому радиусу аВ=![]() 2/те2~а0. Но
величина е2~
2/те2~а0. Но
величина е2~![]() vе (поскольку
кинетическая энергия электрона
порядка потенциальной, то е2/r~тvе2, r~ав, vе2~е4/
vе (поскольку
кинетическая энергия электрона
порядка потенциальной, то е2/r~тvе2, r~ав, vе2~е4/![]() 2). Отсюда получаем σ~ аВ 2, ve~e2/
2). Отсюда получаем σ~ аВ 2, ve~e2/![]() , и время релаксации
, и время релаксации
![]() ~
~![]() ~
~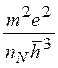
![]() (3.6)
(3.6)
Здесь nN— концентрация нейтральной примеси. Более точная формула, получаемая для водородоподобных атомов, имеет вид
![]() =
= 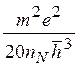
![]() (3.7)
(3.7)
Отметим, что в этом приближении время релаксации не зависит от энергии носителей. Для не водородоподобных атомов такая зависимость появляется (см. подробнее [6]).
Если электрон рассеивается на примесном ионе зарядом Ze, то потенциал такого
взаимодействия есть V(r)~±(Ze2/ε0r)exp(— r/rD), где rD — дебаевский радиус
экранирования,
равный rD ~ (рe/![]() ) (е2/
) (е2/![]() vе)1/2. Такой вид
потенциала получается, если рассмотреть электростатическую задачу о поле иона,
помещенного в среду с диэлектрической проницаемостью
vе)1/2. Такой вид
потенциала получается, если рассмотреть электростатическую задачу о поле иона,
помещенного в среду с диэлектрической проницаемостью ![]() . Уже
из вида потенциала V(r) следует, что он спадает чрезвычайно быстро за счет
экранирования иона примеси электронами. Тем самым опять получается, что сечение
σ~а02 можно брать величиной порядка ав2.
Действительно, оценка rD ~
. Уже
из вида потенциала V(r) следует, что он спадает чрезвычайно быстро за счет
экранирования иона примеси электронами. Тем самым опять получается, что сечение
σ~а02 можно брать величиной порядка ав2.
Действительно, оценка rD ~![]() /ре дает (e2~hve) ve~e2/
/ре дает (e2~hve) ve~e2/![]() , а~
, а~![]() 4/т2е4.
Но
4/т2е4.
Но ![]() , и получаем
, и получаем ![]() =
= 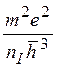 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.