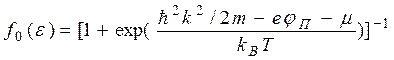Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 30

              (5.6).

Если ввести по определению работу выхода для данной поверхности

         (5.7)

то (5.6) можно представить в виде

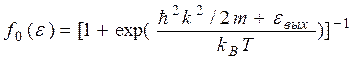                                                                           (5.8)

В табл. 3 приведены величины работы выхода для некоторых элементов.

Таблица 3

Обсудив некоторые свойства поверхностных электронных состояний в твердых телах, обратимся теперь к другой группе Важных явлений — эмиссии электронов из твердого тела под воздействием разного рода факторов: нагрева, сильных электрических полей, излучения и т. п.

5.2. Термоэлектронная эмиссия

Поскольку вероятность выхода электрона из твердого тела возрастает с его энергией, а последняя однозначно связана с температурой тела, попытаемся вычислить поток электронов из твердого тела, зависящий от температуры. Каждый электрон переносит заряд— \е\,поэтому поток электронов есть плотность тока. Считая, что поверхность тела совпадает с плоскостью yOz, запишем х-компоненту плотности электрического тока (см. главу 4):

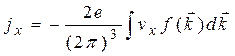                                                                                                                      (5.9)

Здесь 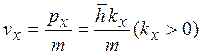 (считаем, что справедлива модель почти свободных электронов, поэтому эффективную массу m_*, везде заменяем на массу свободного электрона m).

Согласно (5.8) и (5.9), получаем

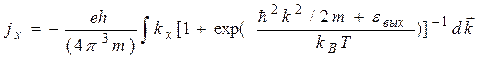(5.10)

При вычислении (5.10) можно воспользоваться следующим. Поскольку W>1эВ, а разумные температуры T<T_m~0,2эB(Т_т-температура плавления), то функция распределения (5.8) переходит в

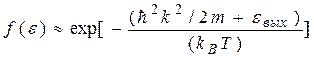                                                                                                (5.11)

Поэтому из (5.10) и (5.11) имеем

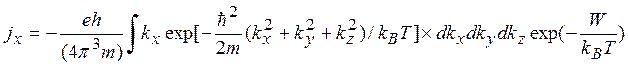(5.12)

Для вычисления (5.12) введем безразмерные коордннаты: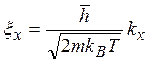, 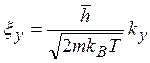_vи     т. д.  Тогда подынтегральное выражение (5.12) можно записать в виде

                  (5.13)

где использовано, что интеграл Пуассона есть   _

                                 ехр (—х²) dx=                       (5.14)

Подставляя (5.13) в (5.12), получим

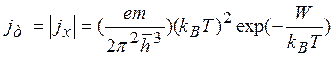                                                                          (5.15)

Выражение   (5.15)   носит  название   формулы   Ричардсона— Дэшмана для термоэлектронного тока  На рис. 5.4 приведены зависимости тока  от температуры для различных значений работы выхода W. Обычно формулу (5.15) записывают в форме

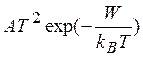 =                                            (5.16)

где А = 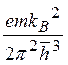 ≈ 120 А/(см²∙К) носит название постоянной Зоммерфельда. Отметим следующее обстоятельство: если масса в выражении (5.15) не совпадает с массой свободного электрона при сложном законе дисперсии, то следует писать в (5.15) эффективную массу т_* Тогд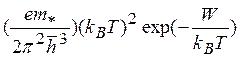а       = , где А = 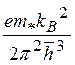≈ 120 (m_*/m)А/(см²∙К)

Подчеркнем, что несмотря на некоторые упрощения, использованные при получении (5.15), эта формула весьма хорошо описывает экспериментальную ситуацию и пригодна в широком диапазоне температур н токов. Теперь сделаем некоторые разъяснения по поводу термоэмиссионных процессов в полупроводниках. Рассматривая энергетическую диаграмму полупроводника (рис. 5.5), примем, как и для металла, что начало отсчета энергии соответствует энергии электрона в вакууме. Тогда из рис. 5.5 следует, что работа выхода в полупроводнике, соответствующая по модулю энергии Ферми, отвечает уровню химического потенциала μ в запрещенной зоне (для невырожденного полупроводника). Однако на этом уровне нет электронов, поэтому кажется неясным, откуда они берутся при эмиссии. Дело, однако, заключается в следующем. В отличие от металлов концентрация носителей в полупроводнике, а значит и положение уровня Ферми, зависят от температуры. Для собственного полупроводника получаем (см. первую часть пособия)

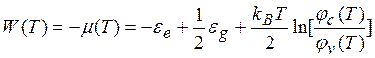                                                                                       (5.16)