где суммирование производится по удельным сопротивлениям определяемым разными механизмами трассеяния. Аддитивный вклад в сопротивление (правило Матиссена) обусловлен независимостью отдельных механизмов рассеяния. Однако следует указать, что это правило может нарушаться. В частности, последнее имеет место для анизотропного рассеяния [8,- 14]. Вместе с тем, для оценок правило Матиссена «работает» в широких пределах и им удобно пользоваться. Обратимся к вкладу в кинетические коэффициенты отдельных механизмов рассеяния, Поскольку σe~τe, λe~τe основной вклад в эти коэффициенты будут давать механизмы с минимальным временем рассеяния (кинетика определяется наиболее быстрыми механизмами). Величины τе для различных процессов удобно сравнивать при высоких и низких температурах.
1. Высокие температуры (T>>θD ). В этом случае на основании приведенных выше соотношений имеем
τee~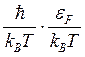 , τep~
, τep~![]() τпр(~τI)~
τпр(~τI)~![]()
Видно, что τee>>τep в
меру εF/kBT>>1.Сдругой стороны, τпр/τee~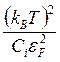 , так
что электрон-электронное рассеяние может быть существенным лишь в
очень чистых образцах. Теперь оценим τпр/τeр~kBT/ciεF. Здесь возможны два варианта:
, так
что электрон-электронное рассеяние может быть существенным лишь в
очень чистых образцах. Теперь оценим τпр/τeр~kBT/ciεF. Здесь возможны два варианта:
а) чистые образцы:
|
(3.54) |
Ci<<![]() ~10-2÷10-4
~10-2÷10-4
В этом случае σe, λeопределяются фононной подсистемой (см. раздел о кинетике фононов), причем σe~T, λe≈const
б) образцы с примесями:
|
(3.55) |
Ci 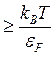 ~10-2÷10-4
~10-2÷10-4
Здесь все определяется рассеянием электронов на примесях и σe≈const, λe~T.
Суммируя оба случая, можно записать
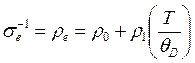 (3.56)
(3.56)
2. Низкие температуры (T<<θD).Для времен релаксации имеем
τee~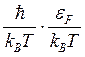 , τepp~
, τepp~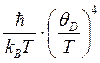
(3.57)
Величина 1/τee всегда мала, так как T<<θD. Соотношения между различными характерными временами имеют вид
τпр /τep(p)~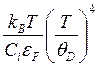 , τпр/τep(ε)~
, τпр/τep(ε)~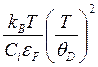 (3.58)
(3.58)
причем τep(p)/τep(ε)~(T/θD)2. Время тер(р> определяет электропроводность (рассеяние импульса), время τвρ(ε) — теплопроводность электронов (рассеяние энергии). При этом, как нетрудно видеть, закон Видемана — Франца нарушается (λe/σe~ τep(ε)/τep(p)). Следует указать, что здесь также возможны два варианта:
а) чистые образцы (Ci<<kBT/εF)
σe~T-5 (3.57)
λe~T-2; (3.60)
б) образцы с примесями (![]() ):
):
σe=const
λe~T
(3.62)
Таким образом, можно записать сопротивление и теплопроводность при низких температурах T<<θD
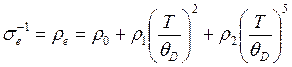 (3.63)
(3.63)
λe-1=AT-1+BT+CT2 (3.64)
Правая часть (3.63) и (3.64) обусловлена соответственно вкладом рассеяния электронов на примесях, на электронах и на фононах. Отметим, что при T→0
сопротивление ρe не стремится к нулю, а остается постоянным (за счет рассеяния на примесях). Такое сопротивление обычно называют остаточным. При высоких температурах имеем случай рассеян^, электронов на фононах, поэтому
ρe=αT
λe=const.
Для иллюстрации полученных результатов на рис. 3.3 показаны качественные зависимости σe, λe для чистых образцу и образцов с примесями (штриховые линии). Помечены области вклада в суммарную теплопроводность электронной и
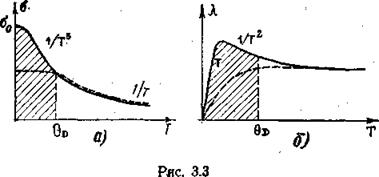
фононной подсистем. Эти качественные зависимости ворительно описывают экспериментальные данные (см. пример, рис. 3.3, а также [8, 10, 13]).
3.4. Термоэлектрические эффекты в твердом теле
Выше были рассмотрены эффекты, связанные с разделённым действием на носители электрического поля и температурного градиента. Теперь обратимся к изучению явлений, связанных с одновременным действием обоих этих факторов. В этом случае уравнение (3.5) сводится к виду
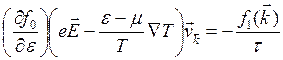 (3.66)
(3.66)
Отсюда находим
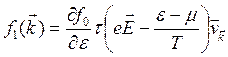 (3.67)
(3.67)
Вычислим плотность электрического тока (сравни раздел 3.3);
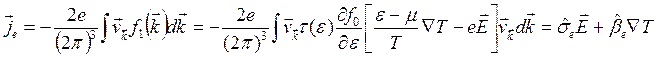 (3.68)
(3.68)
Здесь
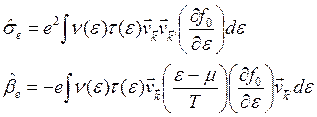
Если ![]() и
и ![]() , то
, то ![]() , откуда
получаем
, откуда
получаем
![]()
Здесь sеесть (3.28) , а bе соответственно
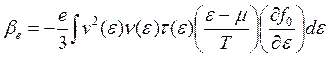
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.